
 如图,在△AOB中,∠A=30°,∠AOB=90°,双曲线y=$\frac{2}{x}$(x>0)经过点B,双曲线y=$\frac{k}{x}$(x<0)经过点A,则k等于-6.
如图,在△AOB中,∠A=30°,∠AOB=90°,双曲线y=$\frac{2}{x}$(x>0)经过点B,双曲线y=$\frac{k}{x}$(x<0)经过点A,则k等于-6. 分析 作AM⊥x轴于M,BN⊥x轴于N,则∠AMB=∠BNO=∠AOB=90°,得出△AOM∽△OBN,由相似三角形的性质即可得出结果,求出$\frac{OA}{OB}$=$\sqrt{3}$,由相似三角形的性质求出△AOM的面积,即可得出k的值.
解答 解:如图所示,作AM⊥x轴于M,BN⊥x轴于N,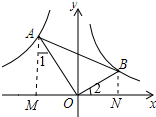 则∠AMB=∠BNO=∠AOB=90°,
则∠AMB=∠BNO=∠AOB=90°,
∴∠1=∠2,
∴△AOM∽△OBN.
∵双曲线y=$\frac{2}{x}$(x>0)经过点B,双曲线y=$\frac{k}{x}$(x<0)经过点A,
∴S△OBN=1,S△AOM=-$\frac{1}{2}$k,
∵∠OAB=30°,∠AOB=90°,
∴∠ABO=60°,
∴$\frac{OA}{OB}$=$\sqrt{3}$,
∴$\frac{{S}_{△AOM}}{{S}_{△OBN}}$=($\sqrt{3}$)2=3,
∴△AOM的面积=3,
∴k=-6.
故答案为:-6.
点评 本题考查的是反比例函数图象上点的坐标特征,通过作辅助线证明三角形相似是解决问题的关键.


 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案科目:初中数学 来源: 题型:选择题
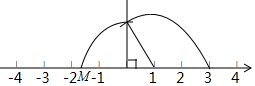 根据图中所示的作图方法,先后得到分别以表示1的点和原点为圆心的两条弧,第二条弧与数轴相交于点M,则点M所表示的数为( )
根据图中所示的作图方法,先后得到分别以表示1的点和原点为圆心的两条弧,第二条弧与数轴相交于点M,则点M所表示的数为( )| A. | -1.7 | B. | -$\sqrt{2}$ | C. | -$\sqrt{3}$ | D. | -$\sqrt{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
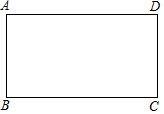 如图,矩形ABCD,点E是边AD上一点,过点E作EF⊥BC,垂足为点F,将△BEF绕着点E逆时针旋转,使点B落在边BC上的点N处,点F落在边DC上的点M处,如果点M恰好是边DC的中点,那么$\frac{AD}{AB}$的值是$\frac{5\sqrt{3}}{6}$.
如图,矩形ABCD,点E是边AD上一点,过点E作EF⊥BC,垂足为点F,将△BEF绕着点E逆时针旋转,使点B落在边BC上的点N处,点F落在边DC上的点M处,如果点M恰好是边DC的中点,那么$\frac{AD}{AB}$的值是$\frac{5\sqrt{3}}{6}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
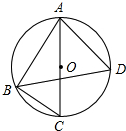 如图,△ABC是⊙O的内接三角形,AC是⊙O的直径,∠C=50°,∠ABC的平分线BD交⊙O于点D,则∠BAD的度数是( )
如图,△ABC是⊙O的内接三角形,AC是⊙O的直径,∠C=50°,∠ABC的平分线BD交⊙O于点D,则∠BAD的度数是( )| A. | 95° | B. | 90° | C. | 85° | D. | 75° |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
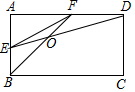 如图,在矩形ABCD中,E、F分别是AB、AD的中点,连接BF、DE交于点O,连接EF,给出如下结论:
如图,在矩形ABCD中,E、F分别是AB、AD的中点,连接BF、DE交于点O,连接EF,给出如下结论:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在一个不透明的袋子中,装有2个红球和1个白球,这些球除了颜色外都相同.如果第一次随机摸出一个小球(不放回),充分搅匀后,第二次再从剩余的两球中随机摸出一个小球,求两次都摸到红球的概率.(用树状图或列表法求解)
在一个不透明的袋子中,装有2个红球和1个白球,这些球除了颜色外都相同.如果第一次随机摸出一个小球(不放回),充分搅匀后,第二次再从剩余的两球中随机摸出一个小球,求两次都摸到红球的概率.(用树状图或列表法求解)查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com