
 如图,在四边形ABCD中,AD∥BC,∠BAD=∠BCD.
如图,在四边形ABCD中,AD∥BC,∠BAD=∠BCD.分析 (1))由AD∥BC,可知∠B+∠BAD=180°,然后再根据∠BAD=∠BCD,证明得∠B+∠BCD=180°,从而可证明AB∥CD;
(2)首先证明∠BAC+∠ADC=180°-∠DAC,然后再证明△HAF≌△CAF,从而可证明:2∠H=180°-∠HAC.
解答 解:(1)∵AD∥BC,
∴∠B+∠BAD=180°.
∵∠BAD=∠BCD,
∴∠B+∠BCD=180°.
∴AB∥CD;
(2)图形如下图所示: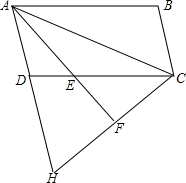
∵AB∥CD,
∴∠BAC=∠ACD.
∴∠BAC+∠ADC=∠ACD+∠ADC=180°-∠DAC.
∵CF⊥AE,
∴∠AFC=∠AFH=90°.
∵AF平分∠DAC,
∴∠HAF=∠CAF.
在△HAF和△CAF中,
$\left\{\begin{array}{l}{∠HAF=∠CAF}\\{AF=AF}\\{∠AFC=∠AFH}\end{array}\right.$,
∴△HAF≌△CAF.
∴∠H=∠HCA.
∴2∠H=∠H+∠HCA=180°-∠HAC.
∴2∠H=∠BAC+∠ADC.
点评 本题主要考查的是平行线的性质,全等三角形的性质和判定、三角形的内角和定理的应用,证得△HAF≌△CAF,从而得到2∠H=∠H+∠HCA=180°-∠HAC是解题的关键.


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:初中数学 来源: 题型:解答题
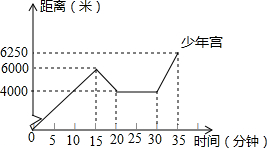 小刚周末骑单车从家出发去少年宫,当他骑了一段路时,想起要买一本书,于是原路返回到刚经过的深圳书城,买到书后继续前往少年宫,如图是他离家的距离与时间的关系示意图,请根据图中提供的信息回答下列问题:
小刚周末骑单车从家出发去少年宫,当他骑了一段路时,想起要买一本书,于是原路返回到刚经过的深圳书城,买到书后继续前往少年宫,如图是他离家的距离与时间的关系示意图,请根据图中提供的信息回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 某班50人参加猜谜语比赛,老师把本班猜谜语活动的情况绘制如图的条形统计图,根据此图,本班猜对谜语个数的中位数和众数分别是( )
某班50人参加猜谜语比赛,老师把本班猜谜语活动的情况绘制如图的条形统计图,根据此图,本班猜对谜语个数的中位数和众数分别是( )| A. | 18,20 | B. | 20,20 | C. | 8,8 | D. | 9,8 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知AC垂直平分BD,∠ABC=∠DAF,DF⊥BD
如图,已知AC垂直平分BD,∠ABC=∠DAF,DF⊥BD查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 增加6m2 | B. | 减少6m2 | C. | 增加9m2 | D. | 减少9m2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,点D以每秒1个单位长度的速度由点A向点B匀速运动,到达B点即停止运动,M,N分别是AD,CD的中点,连接MN,设点D运动的时间为t.
如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,点D以每秒1个单位长度的速度由点A向点B匀速运动,到达B点即停止运动,M,N分别是AD,CD的中点,连接MN,设点D运动的时间为t.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com