
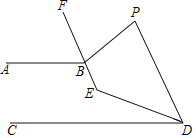
【题目】如图已知AB∥CD,P为直线AB,CD外一点,BF平分∠ABP,DE平分∠CDP,BF的反向延长线交DE于点E.
(1)∠ABP,∠P和∠PDC的数量关系为 ;
(2)若∠BPD=80°,求∠BED的度数;
(3)∠P与∠E的数量关系为 .
【答案】(1)∠ABP=∠P+∠ADC;(2)∠BED=140°;(3)∠BED+![]() P=180°.
P=180°.
【解析】
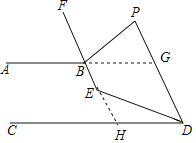
(1)延长AB交PD于G,根据平行线的性质得到∠PGA=∠PDC,根据三角形的外角的性质即可得到结论;
(2)延长FE交CD于H,根据平行线的性质和角平分线的定义即可得到结论;
(3)根据平行线的性质和角平分线的定义即可得到结论.
解:(1)延长AB交PD于G,
∵AG∥CD,
∴∠PGA=∠PDC,
∵∠ABP=∠P+∠AGP,
∴∠ABP=∠P+∠ADC,
故答案为:∠ABP=∠P+∠ADC;
(2)延长FE交CD于H,
∵AB∥CD,
∴∠ABF=∠CHB,
∵BF平分∠ABP,DE平分∠CDP,
∴∠ABF=∠CHB=![]() ABP,∠HDE=
ABP,∠HDE=![]() PDC,
PDC,
∵∠ABP=∠P+∠ADC,
∴∠CHE=![]() (∠P+∠PDC)=40°+∠HDE,
(∠P+∠PDC)=40°+∠HDE,
∵∠CHE=∠HDE+∠DEH,
∴∠DEH=40°,
∴∠BED=180°﹣∠DEH=140°;
(3)由(2)知,∠CHE=![]() (∠P+∠PDC)=
(∠P+∠PDC)=![]() P+∠HDE,
P+∠HDE,
∵∠CHE=∠DEH+∠HDE,
∴∠DEH=![]() ∠P,
∠P,
∴∠BED=180°﹣![]() ∠P.
∠P.
∴∠BED+![]() P=180°.
P=180°.
故答案为:∠BED+![]() P=180°.
P=180°.


科目:初中数学 来源: 题型:
【题目】如图,抛物线y=x2+bx+c与x轴交于A,B两点,且点A在点B的左侧,直线y=﹣x﹣1与抛物线交于A,C两点,其中点C的横坐标为2.
(1)求二次函数的解析式;
(2)P是线段AC上的一个动点,过点P作y轴的平行线交抛物线于点E,求线段PE长度的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,∠BAD、∠ABC的平分线AF、BG分别与线段CD交于点F、G,
AF与BG交于点E.

(1)求证:AF⊥BG,DF=CG;
(2)若AB=10,AD=6,AF=8,求FG和BG的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
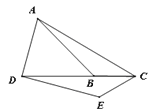
【题目】如图,在△ABC中,∠ACB=30°,将△ABC绕点C逆时针旋转得到△DEC,点A的对应点D恰好落在线段CB的延长线上,连接AD,若∠ADE=90°,则∠BAD=_________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的顶点都在网格点上,其中A(2,﹣1),B(4,3),C(1,2)
(1)将△ABC先向左平移2个单位长度,再向上平移1个单位长度,得到△A′B′C′,ABC的对应点分别为A′B′C′,画出△A′B′C′,并写出A′B′C′的坐标;
(2)求△ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校组织七、八年级全体同学参观八路军太行纪念馆(位于山西省长治市武乡县城).七年级租用45座大巴车![]() 辆,55座大巴车
辆,55座大巴车![]() 辆;八年级租用30座中巴车
辆;八年级租用30座中巴车![]() 辆,55座大巴车
辆,55座大巴车![]() 辆.当每辆车恰好坐满时:
辆.当每辆车恰好坐满时:

(1)用含有![]() ,
,![]() 的代数式分别表示七、八年级各有学生数.
的代数式分别表示七、八年级各有学生数.
(2)用含有![]() ,
,![]() 的代数式表示七、八年级共有多少学生?
的代数式表示七、八年级共有多少学生?
(3)当![]() ,
,![]() 时,该学校七、八年级共有多少学生?
时,该学校七、八年级共有多少学生?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的袋子中装有红、白两种颜色的小球,这些球除颜色外完全相同,其中红球有![]() 个,若从中随机摸出一个球,这个球是白球的概率为
个,若从中随机摸出一个球,这个球是白球的概率为![]() .
.
(![]() )请直接写出袋子中白球的个数.
)请直接写出袋子中白球的个数.
(![]() )随机摸出一个球后,放回并搅匀,再随机摸出一个球,求两次都摸到相同颜色的小球的概率.(请结合树状图或列表解答)
)随机摸出一个球后,放回并搅匀,再随机摸出一个球,求两次都摸到相同颜色的小球的概率.(请结合树状图或列表解答)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下面三行数:
①-3,9,-27,81,-243,729,…;
②0,12,-24,84,-240,732,…;
③-1,3,-9,27,-81,243,….
(1)第①行数有什么规律?
(2)第②行数与第①行数有什么关系?
(3)第③行数与第①行数有什么关系?
(4)取每行数的第10个数,计算这三个数的和.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为灾区开展了“献出我们的爱”赈灾捐款活动,九年级(1)班50名同学积极参加了这次赈灾捐款活动,因不慎,表中数据有一处被墨水污染,已无法看清,但已知全班平均每人捐款38元.
捐款(元) | 10 | 15 | 30 | 50 | 60 | |
人数 | 3 | 6 | 11 | 11 | 13 | 6 |
(1)根据以上信息可知,被污染处的数据为 .
(2)该班捐款金额的众数为 ,中位数为 .
(3)如果用九年级(1)班捐款情况作为一个样本,请估计全校2000人中捐款在40元以上(包括40元)的人数是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com