
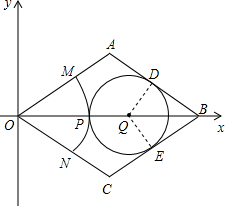
 ��ͼ������OABC�Ķ���O������ԭ�㣬����B��x����������ϣ�OA������ֱ��Ϊy=$\frac{\sqrt{3}}{3}$x��AB������ֱ��Ϊy=-$\frac{\sqrt{3}}{3}$x+2��
��ͼ������OABC�Ķ���O������ԭ�㣬����B��x����������ϣ�OA������ֱ��Ϊy=$\frac{\sqrt{3}}{3}$x��AB������ֱ��Ϊy=-$\frac{\sqrt{3}}{3}$x+2������ ��1����Ϊ����OABC�Ķ���O������ԭ�㣬����B��x����������ϣ�OA����ֱ��y=$\frac{\sqrt{3}}{3}$x�ϣ�AB����ֱ��y=-$\frac{\sqrt{3}}{3}$x+2�ϣ�����A����ֱ�ߵĽ��㣮����ֱ�ߵĽ���ʽ�������õ������飬��֮���ɵõ�A������A��$\sqrt{3}$��1�����������εĶԳ��Լ��ɵõ���AOC�Ķ�����
��2����Ϊ��Q�ֱ����AB��BC�����ڵ�D��E�����Կ�����QD��QE����QD��AB��QE��BC��QD=QE���Ӷ��жϵ�Q�ڡ�ABC��ƽ�����ϣ��������εĶԽ���ƽ��һ���ڶԽǿ�֪��Q��OB�ϣ�����Ϊ��Q�뻡MN�����ڵ�P������Rt��QDB�У���QBD=30�㣬����QB=2QD=2r����y+3r=2$\sqrt{3}$���������ɵõ���Ҫ��Ľ���ʽ��
��3����Ϊ��OΪԲ�ġ�OAΪ�뾶������OAC����AC�ij�Ϊ$\frac{2}{3}$�У�����µġ�Q������������뾶ΪR����2��R=$\frac{2}{3}$�У�����R=$\frac{1}{3}$���ɣ�2��֪����ʱOA=y=2�����Q�İ뾶����R���ܽ���һ��Բ��ʹ����������OAC�պ�Χ��һ��Բ��
���  �⣺��1��������ɵã�$\left\{\begin{array}{l}{y=\frac{\sqrt{3}}{3}x}\\{y=-\frac{\sqrt{3}}{3}x+2}\end{array}\right.$��
�⣺��1��������ɵã�$\left\{\begin{array}{l}{y=\frac{\sqrt{3}}{3}x}\\{y=-\frac{\sqrt{3}}{3}x+2}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{x=\sqrt{3}}\\{y=1}\end{array}\right.$��
��A��$\sqrt{3}$��1����
��tan��AOB=$\frac{\sqrt{3}}{3}$���ʡ�AOC=60�㣬
�ʴ�Ϊ����$\sqrt{3}$��1����60�㣻
��2������QD��QE����QD��AB��QE��BC��
��QD=QE��
���Q�ڡ�ABC��ƽ�����ϣ�
�֡�OABC�����Σ�
���Q��OB�ϣ�
���Q�뻡MN�����ڵ�P��
��Rt��QDB�У���QBD=30�㣬
��QB=2QD=2r��
��y+3r=2$\sqrt{3}$��
��y=2$\sqrt{3}$��
��y��0��
��2$\sqrt{3}$-3r��0��
��r��$\frac{2\sqrt{3}}{3}$��
��A��$\sqrt{3}$��1��
��AO=2��
��2$\sqrt{3}$-3r��2��
��ã�$\frac{2\sqrt{3}-2}{3}$��r��
��$\frac{2\sqrt{3}-2}{3}$��r��$\frac{2\sqrt{3}}{3}$��
��3�����ԣ�
���ɣ���AC�ij�Ϊ$\frac{2}{3}$�У�
����µġ�Q������������뾶ΪR����2��R=$\frac{2}{3}$�У�
��R=$\frac{1}{3}$��
�ɣ�2��֪����ʱOA=y=2�����Q�İ뾶R=$\frac{2\sqrt{3}-2}{3}$��$\frac{1}{3}$��
���ܽ���һ��Բ��ʹ����������OAC�պ�Χ��һ��Բ��
���� ������Ҫ������Բ���ۺϣ���������ϸ�������⣬���ͼ�Σ��������ε����ʡ����ߵ����ʼ��ɽ�����⣮


 ѧ���������ν��Ͼ���ѧ������ϵ�д�
ѧ���������ν��Ͼ���ѧ������ϵ�д� Happy holiday���ּ��������ҵ�㶫���������ϵ�д�
Happy holiday���ּ��������ҵ�㶫���������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
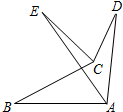 ��ͼ����ABC����ADC���ҡ�BAD��ƽ����AE���BCD��ƽ����CE���ڵ�E�����AEC���ADC����ABC֮����ڵĵ�����ϵ�ǣ�������
��ͼ����ABC����ADC���ҡ�BAD��ƽ����AE���BCD��ƽ����CE���ڵ�E�����AEC���ADC����ABC֮����ڵĵ�����ϵ�ǣ�������| A�� | ��AEC=��ABC-2��ADC | B�� | ��AEC=$\frac{��ABC-��ADC}{2}$ | ||
| C�� | ��AEC=$\frac{1}{2}$��ABC-��ADC | D�� | ��AEC=$\frac{��ABC-��ADC}{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
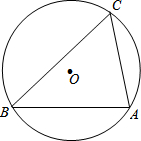 ����һ�������Σ����������ڽǵĶ����ֱ�Ϊx�㡢y���z�㣬��x��y��z����x2+y2=z2�����Ƕ������������Ϊ���������Σ�
����һ�������Σ����������ڽǵĶ����ֱ�Ϊx�㡢y���z�㣬��x��y��z����x2+y2=z2�����Ƕ������������Ϊ���������Σ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
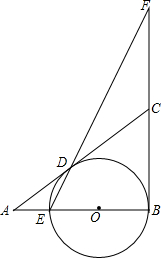 ��ͼ���ڡ�ABC�У���B=90�㣬O��AB��һ�㣬��OΪԲ�ģ�OBΪ�뾶��Բ��AB���ڵ�E����AC���ڵ�D������ED�����ӳ���BC���ӳ����ڵ�F��
��ͼ���ڡ�ABC�У���B=90�㣬O��AB��һ�㣬��OΪԲ�ģ�OBΪ�뾶��Բ��AB���ڵ�E����AC���ڵ�D������ED�����ӳ���BC���ӳ����ڵ�F���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ���ڡ�ABC�У�D��E�ֱ��DZ�BC��AB���е㣬AD��CE�ཻ��F����$\frac{DF}{AD}$=��������
��ͼ���ڡ�ABC�У�D��E�ֱ��DZ�BC��AB���е㣬AD��CE�ཻ��F����$\frac{DF}{AD}$=��������| A�� | $\frac{1}{2}$ | B�� | $\frac{1}{3}$ | C�� | $\frac{1}{4}$ | D�� | $\frac{2}{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{x}{2}$+$\frac{y}{4}$=-1 | B�� | xy+z=5 | C�� | 2x2+3y-5=0 | D�� | 2x+$\frac{1}{y}$=2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��ֱ��ƽ�У�ͬλ����� | B�� | ƽ���ı��εĶԽ�����ƽ�� | ||
| C�� | ���ε���������� | D�� | �����ε��ĸ��Ƕ���ֱ�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com