
【题目】AB∥CD,点C在点D的右侧,∠ABC 、∠ADC的平分线交于点E(不与B,D点重合).∠ABC=n°,∠ADC=80°.
(1)若点B在点A的左侧,求∠BED的度数(用含n的代数式表示);
(2)将(1)中的线段BC沿DC方向平移,当点B移动到点A右侧时,请画出图形并判断∠BED的度数是否改变.若改变,请求出∠BED的度数(用含n的代数式表示);若不变,请说明理由.

【答案】(1)∠BED=![]() n°+40°;(2)∠BED的度数改变,∠BED=220°﹣
n°+40°;(2)∠BED的度数改变,∠BED=220°﹣![]() n°.
n°.
【解析】试题分析:(1)如图1,过点E作EF∥AB,根据平行线性质可得∠ABE=∠BEF,∠CDE=∠DEF,再由角平分线定义得出∠ABE=![]() ∠ABC
∠ABC![]() =n°,∠CDE=
=n°,∠CDE=![]() ∠ADC=40°,代入∠BED=∠BEF+∠DEF即可求得答案;
∠ADC=40°,代入∠BED=∠BEF+∠DEF即可求得答案;
(2)如图2,过点E作EF∥AB,根据角平分线定义可得∠ABE=![]() ∠ABC=
∠ABC=![]() n°,∠CDE=
n°,∠CDE=![]() ∠ADC=40°,再由平行线性质可得∠BEF=180°﹣∠ABE=180°﹣
∠ADC=40°,再由平行线性质可得∠BEF=180°﹣∠ABE=180°﹣![]() n°,∠CDE=∠DEF=40°,代入∠BED=∠BEF+∠DEF即可求得答案.
n°,∠CDE=∠DEF=40°,代入∠BED=∠BEF+∠DEF即可求得答案.
试题解析:解:(1)过点E作EF∥AB,
∵AB∥CD,
∴AB∥CD∥EF,
∴∠ABE=∠BEF,∠CDE=∠DEF,
∵BE平分∠ABC,DE平分∠ADC,∠ABC=n°,∠ADC=80°,
∴∠ABE=![]() ∠ABC=
∠ABC=![]() n°,∠CDE=
n°,∠CDE=![]() ∠ADC=40°,
∠ADC=40°,
∴∠BED=∠BEF+∠DEF=![]() n°+40°;
n°+40°;
(2)∠BED的度数改变,
过点E作EF∥AB,如图,
∵BE平分∠ABC,DE平分∠ADC,∠ABC=n°,∠ADC=80°,
∴∠ABE=![]() ∠ABC=
∠ABC=![]() n°,∠CDE=
n°,∠CDE=![]() ∠ADC=40°,
∠ADC=40°,
∵AB∥CD,
∴AB∥CD∥EF,
∴∠BEF=180°﹣∠ABE=180°﹣![]() n°,∠CDE=∠DEF=40°,
n°,∠CDE=∠DEF=40°,
∴∠BED=∠BEF+∠DEF=180°﹣![]() n°+40°=220°﹣
n°+40°=220°﹣![]() n°.
n°.



 新思维寒假作业系列答案
新思维寒假作业系列答案科目:初中数学 来源: 题型:
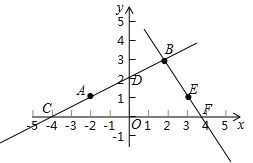
【题目】连接AB,直线AB与x轴交于点C,与y轴交于点D,平面内有一点E(3,1),直线BE与x轴交于点F.直线AB的解析式记作y1=kx+b,直线BE解析式记作y2=mx+t.求:
(1)直线AB的解析式△BCF的面积;
(2)当x 时,kx+b>mx+t;
当x 时,kx+b<mx+t;
当x 时,kx+b=mx+t;
(3)在x轴上有一动点H,使得△OBH为等腰三角形,求H的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列问题用到推理的是( )
A. 根据x=1,y=1,得x=y
B. 观察得到的四边形有四个内角
C. 老师告诉了我们关于金字塔的许多奥秘
D. 由公理知道过两点有且只有一条直线
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】买一个足球需要m元,买一个篮球需要n元,则买4个足球、7个篮球共需要( )
A. (7m+4n)元 B. 28mn元 C. (4m+7n)元 D. 11mn元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据深圳统计局公布数据,2015年深圳公共财政收入达7240亿元,同比增长30.2%,数据“7240亿”用科学记数法表示为( )
A.0.724×1013 B.7.24×1012 C.7.24×1011 D.72.4×1011
查看答案和解析>>
科目:初中数学 来源: 题型:
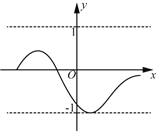
【题目】对某一个函数给出如下定义:若存在实数M>0,对于任意的函数值y,都满足﹣M≤y≤M,则称这个函数是有界函数,在所有满足条件的M中,其最小值称为这个函数的边界值.例如,如图中的函数是有界函数,其边界值是1.
(1)分别判断函数 y=![]() (x>0)和y=x+1(﹣4≤x≤2)是不是有界函数?若是有界函数,求其边界值;
(x>0)和y=x+1(﹣4≤x≤2)是不是有界函数?若是有界函数,求其边界值;
(2)若函数y=﹣x+1(a≤x≤b,b>a)的边界值是2,且这个函数的最大值也是2,求b的取值范围;
(3)将函数 y=x2(﹣1≤x≤m,m≥0)的图象向下平移m个单位,得到的函数的边界值是t,当m在什么范围时,满足![]() ≤t≤1?
≤t≤1?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,OABC是平行四边形,对角线OB在y轴正半轴上,位于第一象限的点A和第二象限的点C分别在双曲线![]() 和
和![]() 的一支上,分别过点A、C作x轴的垂线,垂足分别为M和N,则有以下的结论:
的一支上,分别过点A、C作x轴的垂线,垂足分别为M和N,则有以下的结论:
①![]() ;②阴影部分面积是
;②阴影部分面积是![]() (k1+k2);③当∠AOC=90°时,|k1|=|k2|;④若OABC是菱形,则两双曲线既关于x轴对称,也关于y轴对称.其中正确的结论是( )
(k1+k2);③当∠AOC=90°时,|k1|=|k2|;④若OABC是菱形,则两双曲线既关于x轴对称,也关于y轴对称.其中正确的结论是( )

A.①②③ B.②④ C.①③④ D.①④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com