
【题目】如图,![]() 中,
中,![]() ,
,![]() 于
于![]() ,
,![]() 平分
平分![]() ,且
,且![]() 于
于![]() ,与
,与![]() 相交于点
相交于点![]() ,
,![]() 于
于![]() ,交
,交![]() 于
于![]() ,下列结论:①
,下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .其中正确的是( )
.其中正确的是( )

A.①②B.①③C.①②③D.①②③④
【答案】C
【解析】
根据∠ABC=45°,CD⊥AB可得出BD=CD,利用AAS判定Rt△DFB≌Rt△DAC,从而得出DF=AD,BF=AC.则CD=CF+AD,即AD+CF=BD;再利用AAS判定Rt△BEA≌Rt△BEC,得出CE=AE=![]() AC,又因为BF=AC所以CE=
AC,又因为BF=AC所以CE=![]() AC=
AC=![]() BF;连接CG.因为△BCD是等腰直角三角形,即BD=CD.又因为DH⊥BC,那么DH垂直平分BC.即BG=CG;在Rt△CEG中,CG是斜边,CE是直角边,所以CE<CG.即AE<BG.
BF;连接CG.因为△BCD是等腰直角三角形,即BD=CD.又因为DH⊥BC,那么DH垂直平分BC.即BG=CG;在Rt△CEG中,CG是斜边,CE是直角边,所以CE<CG.即AE<BG.
∵CD⊥AB,∠ABC=45°,
∴△BCD是等腰直角三角形.
∴BD=CD.故①正确;
在Rt△DFB和Rt△DAC中,
∵∠DBF=90°-∠BFD,∠DCA=90°-∠EFC,且∠BFD=∠EFC,
∴∠DBF=∠DCA.
又∵∠BDF=∠CDA=90°,BD=CD,
∴△DFB≌△DAC.
∴BF=AC;DF=AD.
∵CD=CF+DF,
∴AD+CF=BD;故②正确;
在Rt△BEA和Rt△BEC中
∵BE平分∠ABC,
∴∠ABE=∠CBE.
又∵BE=BE,∠BEA=∠BEC=90°,
∴Rt△BEA≌Rt△BEC.
∴CE=AE=![]() AC.
AC.
又由(1),知BF=AC,
∴CE=![]() AC=
AC=![]() BF;故③正确;
BF;故③正确;
连接CG.

∵△BCD是等腰直角三角形,
∴BD=CD
又DH⊥BC,
∴DH垂直平分BC.∴BG=CG
在Rt△CEG中,
∵CG是斜边,CE是直角边,
∴CE<CG.
∵CE=AE,
∴AE<BG.故④错误.
故选C.


 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案科目:初中数学 来源: 题型:
【题目】某电信公司手机的通讯卡有![]() ,
,![]() 两种业务类型:
两种业务类型:![]() 类卡收费标准是:不管通话时间多长,每部手机每月必须缴月租费12元,另外,通话费按0.2元/分钟计;
类卡收费标准是:不管通话时间多长,每部手机每月必须缴月租费12元,另外,通话费按0.2元/分钟计;![]() 类卡收费标准是:没有月租,但通话费按0.25元/分钟计.如图所示,是每月应缴费用
类卡收费标准是:没有月租,但通话费按0.25元/分钟计.如图所示,是每月应缴费用![]() (元)与通话时间
(元)与通话时间![]() (分钟)之间的函数图象.下列结论:
(分钟)之间的函数图象.下列结论:
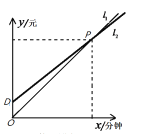
①图中![]() 是
是![]() 类卡的收费方式所表示的函数图象;
类卡的收费方式所表示的函数图象;
②若李海本月的通话时间为180分钟,则他选择![]() 类卡省钱;
类卡省钱;
③若本月李海预缴了100元的话费,则他选择![]() 类卡划算;
类卡划算;
④若![]() 类卡比
类卡比![]() 类卡的话费多10元,则
类卡的话费多10元,则![]() 类卡和
类卡和![]() 类卡的通话时间都是40分钟或
类卡的通话时间都是40分钟或![]() 类卡比
类卡比![]() 类卡的通话时间多40分钟且
类卡的通话时间多40分钟且![]() 类卡和
类卡和![]() 类卡的通话时间分别为240分钟和200分钟.其中正确的结论有( )
类卡的通话时间分别为240分钟和200分钟.其中正确的结论有( )
A.①②③④B.②③④C.②③D.②④
查看答案和解析>>
科目:初中数学 来源: 题型:
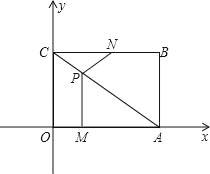
【题目】如图,平面直角坐标系中,四边形OABC为矩形,点A,B的坐标分别为(4,0),(4,3),动点M,N分别从O,B同时出发.以每秒1个单位的速度运动.其中,点M沿OA向终点A运动,点N沿BC向终点C运动.过点M作MP⊥OA,交AC于P,连接NP,已知动点运动了x秒.
(1)求P点的坐标(用含x的代数式表示);
(2)试求△NPC面积S的表达式,并求出面积S的最大值及相应的x值;
(3)设四边形OMPC的面积为S1,四边形ABNP的面积为S2,请你就x的取值范围讨论S1与S2的大小关系并说明理由;
(4)当x为何值时,△NPC是一个等腰三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,BC为⊙O的切线,D为⊙O上的一点,CD=CB,延长CD交BA的延长线于点E.
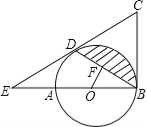
(1)求证:CD为⊙O的切线;
(2)若BD的弦心距OF=1,∠ABD=30°,求图中阴影部分的面积.(结果保留π)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形ABCD中,∠A=140°,∠D=80°.

(1)如图1,若∠B=∠C,试求出∠C的度数;
(2)如图2,若∠ABC的角平分线BE交DC于点E,且BE∥AD,试求出∠C的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
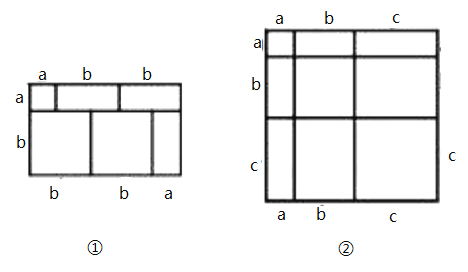
【题目】我们知道,对于一个图形,通过2种不同的方法计算它的面积时,可以得到一个数学等式.例如图①可以得到![]() ,请解答下列问题:
,请解答下列问题:
(1)写出图②中所表示的等式: ;
(2)利用(1)中所得到的结论,解决下面的问题:已知![]() ,
,![]() ,求
,求![]() 的值;
的值;
(3)小明同学用2张边长为![]() 的正方形纸片、3张边长为
的正方形纸片、3张边长为![]() 的正方形纸片,5张边长分别为
的正方形纸片,5张边长分别为![]() 的长方形纸片拼出了一个长方形,那么该长方形较长一边的长为多少?
的长方形纸片拼出了一个长方形,那么该长方形较长一边的长为多少?
(4)小明同学又用![]() 张边长为
张边长为![]() 的正方形纸片,
的正方形纸片,![]() 张边长为
张边长为![]() 的正方形纸片、
的正方形纸片、![]() 张边长分别为
张边长分别为![]() 的长方形纸片拼出了一个面积为
的长方形纸片拼出了一个面积为![]() 的长方形,请问一共用掉多少张纸片?
的长方形,请问一共用掉多少张纸片?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() 是边
是边![]() 上的中线,
上的中线,![]() 是
是![]() 的中点,过点
的中点,过点![]() 作
作![]() 的平行线与
的平行线与![]() 的延长线相交于点
的延长线相交于点![]() ,连接
,连接![]() .
.
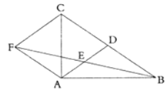
(1)求证:四边形![]() 为平行四边形;
为平行四边形;
(2)若![]() ,请写出图中所有与线段
,请写出图中所有与线段![]() 相等的线段(线段
相等的线段(线段![]() 除外).
除外).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A.B在反比例函数y=![]() 的图象上,且点A,B的横坐标分别为a,2a(a<0),若S△AOB=3,则k的值为( )
的图象上,且点A,B的横坐标分别为a,2a(a<0),若S△AOB=3,则k的值为( )
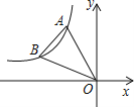
A.5B.-5C.4D.-4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com