
 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案科目:初中数学 来源: 题型:解答题
 问题:探究一次函数y=kx+k+2(k是不为0常数)图象的共性特点,探究过程:小明尝试把x=-1代入时,发现可以消去k,竟然求出了y=2.老师问:结合一次函数图象,这说明了什么?小组讨论得出:无论k取何值,一次函数y=kx+k+2的图象一定经过定点(-1,2),老师:如果一次函数的图象是经过某一个定点的直线,那么我们把像这样的一次函数的图象定义为“点旋转直线”.已知一次函数y=(k+3)x+(k-1)的图象是“点旋转直线”
问题:探究一次函数y=kx+k+2(k是不为0常数)图象的共性特点,探究过程:小明尝试把x=-1代入时,发现可以消去k,竟然求出了y=2.老师问:结合一次函数图象,这说明了什么?小组讨论得出:无论k取何值,一次函数y=kx+k+2的图象一定经过定点(-1,2),老师:如果一次函数的图象是经过某一个定点的直线,那么我们把像这样的一次函数的图象定义为“点旋转直线”.已知一次函数y=(k+3)x+(k-1)的图象是“点旋转直线”查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
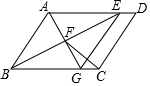 已知:如图,在平行四边形ABCD中,∠ABC的平分线交AD于点E,过点A作BE的垂线交BE于点F,交BC于点G,连接EG,CF.
已知:如图,在平行四边形ABCD中,∠ABC的平分线交AD于点E,过点A作BE的垂线交BE于点F,交BC于点G,连接EG,CF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
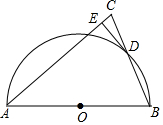 如图,在△ABC中,AB=AC,以AB为直径作半圆O交BC于点D,过点D作DE⊥AC,垂足为E.
如图,在△ABC中,AB=AC,以AB为直径作半圆O交BC于点D,过点D作DE⊥AC,垂足为E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知点A在反比例函数y=$\frac{k}{x}$(x<0)上,作Rt△ABC,点D为斜边AC的中点,连DB并延长交y轴于点E,若△BCE的面积为8.
如图,已知点A在反比例函数y=$\frac{k}{x}$(x<0)上,作Rt△ABC,点D为斜边AC的中点,连DB并延长交y轴于点E,若△BCE的面积为8.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com