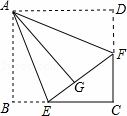
如图，点E、F分别是正方形纸片ABCD的边BC、CD上一点，将正方形纸片ABCD分别沿AE、AF折叠，使得点B、D恰好都落在点G处，且EG=2，FG=3，则正方形纸片ABCD的边长为 ．
阅读快车系列答案科目：初中数学 来源： 题型：
【问题】如图1、2是底面为1cm，母线长为2cm的圆柱体和圆锥体模型．现要用长为2πcm，宽为4cm的长方形彩纸（如图3）装饰圆柱、圆锥模型表面．已知一个圆柱和一个圆锥模型为一套，长方形彩纸共有122张，用这些纸最多能装饰多少套模型呢？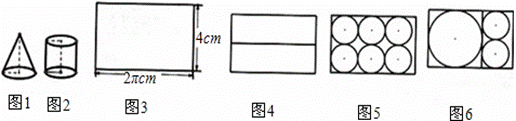
【对话】老师：“长方形纸可以怎么裁剪呢？”
学生甲：“可按图4方式裁剪出2张长方形．”
学生乙：“可按图5方式裁剪出6个小圆．”
学生丙：“可按图6方式裁剪出1个大圆和2个小圆．”
老师：尽管还有其他裁剪方法，但为裁剪方便，我们就仅用这三位同学的裁剪方法！
【解决】（1）计算：圆柱的侧面积是 4πcm2，圆锥的侧面积是 2cm2．
（2）1张长方形彩纸剪拼后最多能装饰 2个圆锥模型；5张长方形彩纸剪拼后最多能装饰 6个圆柱体模型．
（3）求用122张彩纸对多能装饰的圆锥、圆柱模型套数．
查看答案和解析>>
科目：初中数学 来源： 题型：
下列说法不正确的是（ ）
|
| A． | 某种彩票中奖的概率是 |
|
| B． | 了解一批电视机的使用寿命适合用抽样调查 |
|
| C． | 若甲组数据的标准差S甲=0.31，乙组数据的标准差S乙=0.25，则乙组数据比甲组数据稳定 |
|
| D． | 在一个装有白球和绿球的袋中摸球，摸出黑球是不可能事件 |
查看答案和解析>>
科目：初中数学 来源： 题型：
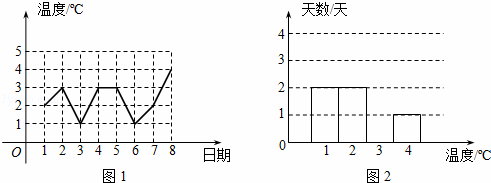
图1是某城市三月份1至8日的日最高气温随时间变化的折线统计图，小刚根据图1将数据统计整理后制成了图2．
根据图中信息，解答下列问题：
（1）将图2补充完整；
（2）这8天的日最高气温的中位数是 ℃；
（3）计算这8天的日最高气温的平均数．
查看答案和解析>>
科目：初中数学 来源： 题型：
如图，在平面直角坐标系中，O是坐标原点，直线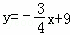
与x轴，y轴分别交于B，C两点，抛物线
经过B，C两点，与x轴的另一个交点为点A，动点P从点A出发沿AB以每秒3个单位长度的速度向点B运动，运动时间为t（0＜t＜5）秒．
（1）求抛物线的解析式及点A的坐标；
（2）以OC为直径的⊙O′与BC交于点M，当t为何值时，PM与⊙O′相切？请说明理由．
（3）在点P从点A出发的同时，动点Q从点B出发沿BC以每秒3个单位长度的速度向点C运动，动点N从点C出发沿CA以每秒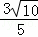
个单位长度的速度向点A运动，运动时间和点P相同．
①记△BPQ的面积为S，当t为何值时，S最大，最大值是多少？
②是否存在△NCQ为直角三角形的情形？若存在，求出相应的t值；若不存在，请说明理由．
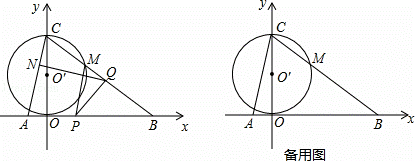
查看答案和解析>>
科目：初中数学 来源： 题型：
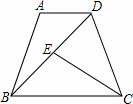
已知：如图，在等腰梯形ABCD中，AD∥BC，∠BDC=∠BCD，点E是线段BD上一点，且BE=AD．
（1）证明：△ADB≌△EBC；
（2）直接写出图中所有的等腰三角形．
查看答案和解析>>
科目：初中数学 来源： 题型：
某种出租车的收费标准：起步价7元（即行驶距离不超过3 km都需付7元车费），超过3 km后，每增加1 km，加收2.4元（不足1 km按1 km计）．某人乘这种出租车从甲地到乙地共付车费19元，那么甲地到乙地路程的最大值是（ ）
A．5 km B．7 km C．8 km D．15 km
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
，买1000张该种彩票一定会中奖