
【题目】阅读以下材料:
对数的创始人是苏格兰数学家纳皮尔(J.Nplcr,1550﹣1617年),纳皮尔发明对数是在指数书写方式之前,直到18世纪瑞士数学家欧拉(Evlcr,1707﹣1783年)才发现指数与对数之间的联系.
对数的定义:一般地,若![]() (
(![]() 且
且![]() ),那么
),那么![]() 叫做以
叫做以![]() 为底
为底![]() 的对数,记作
的对数,记作![]() ,比如指数式
,比如指数式![]() 可以转化为对数式
可以转化为对数式![]() ,对数式
,对数式![]() ,可以转化为指数式
,可以转化为指数式![]() .
.
我们根据对数的定义可得到对数的一个性质:
![]() (
(![]() ,
,![]() ,
,![]() ,
,![]() ),理由如下:
),理由如下:
设![]() ,
,![]() ,则
,则![]() ,
,![]() ,
,
∴![]() ,由对数的定义得
,由对数的定义得![]()
又∵![]()
∴![]()
根据阅读材料,解决以下问题:
(1)将指数式![]() 转化为对数式________;
转化为对数式________;
(2)求证:![]() (
(![]() ,
,![]() ,
,![]() ,
,![]() )
)
(3)拓展运用:计算![]() ________.
________.
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:初中数学 来源: 题型:
【题目】如图,风车的支杆OE垂直于桌面,风车中心O到桌面的距离OE为25cm,小小风车在风吹动下绕着中心O不停地转动,转动过程中,叶片端点A、B、C、D在同一圆O上,已知⊙O的半径为10cm,
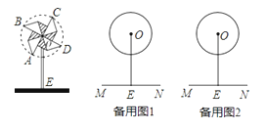
(1)风车在转动过程中,当∠AOE=30°时,求点A到桌面的距离.
(2)在风车转动一周的过程中,求点A相对于桌面的高度不超过20cm所经过的路线长.
查看答案和解析>>
科目:初中数学 来源: 题型:
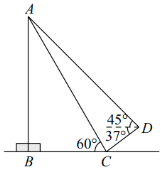
【题目】某校创客社团计划利用新购买的无人机设备测量学校旗杆![]() 的高.他们先将无人机放在旗杆前的点
的高.他们先将无人机放在旗杆前的点![]() 处(无人机自身的高度忽略不计),测得此时点
处(无人机自身的高度忽略不计),测得此时点![]() 的仰角为
的仰角为![]() ,因为旗杆底部有台阶,所以不能直接测出垂足
,因为旗杆底部有台阶,所以不能直接测出垂足![]() 到点
到点![]() 的距离.无人机起飞后,被风吹至点
的距离.无人机起飞后,被风吹至点![]() 处,此时无人机距地面的高度为3米,测得此时点
处,此时无人机距地面的高度为3米,测得此时点![]() 的俯角为
的俯角为![]() ,点
,点![]() 的仰角为
的仰角为![]() ,且点
,且点![]() ,
,![]() ,
,![]() 在同一平面内,求旗杆
在同一平面内,求旗杆![]() 的高度.(计算结果精确到0.1米,参考数据:
的高度.(计算结果精确到0.1米,参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果三角形的两个内角α与β满足2α+β=90°,那么我们称这样的三角形为“准互余三角形”.
(1)若△ABC是“准互余三角形”,∠C>90°,∠A=60°,则∠B= °;
(2)如图①,在Rt△ABC中,∠ACB=90°,AC=4,BC=5.若AD是∠BAC的平分线,不难证明△ABD是“准互余三角形”.试问在边BC上是否存在点E(异于点D),使得△ABE也是“准互余三角形”?若存在,请求出BE的长;若不存在,请说明理由.
(3)如图②,在四边形ABCD中,AB=7,CD=12,BD⊥CD,∠ABD=2∠BCD,且△ABC是“准互余三角形”,求对角线AC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若抛物线![]() 与
与![]() 轴两个交点间的距离为2,称此抛物线为定弦抛物线,已知某定弦抛物线的对称轴为直线
轴两个交点间的距离为2,称此抛物线为定弦抛物线,已知某定弦抛物线的对称轴为直线![]() ,将此抛物线向下平移3个单位,得到的抛物线过点( )
,将此抛物线向下平移3个单位,得到的抛物线过点( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
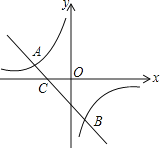
【题目】如图,已知![]() 、
、![]() 是一次函数
是一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象的两个交点.
的图象的两个交点.
(1)求反比例函数和一次函数的表达式;
(2)根据图象写出使一次函数的函数值小于反比例函数的函数值的x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用适当的方法解下列方程.
(1)(2x+3)2 -16=0
(2)3x2+x-1=0
(3)3x(x-1)=2-2x
(4)9(3x-1)2 =(2-x)2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com