
【题目】如图,在△ABC中,以AB为直径的⊙O分别交AC,BC于点D,E,点F在AC的延长线上,且AC=CF,∠CBF=∠CFB. 
(1)求证:直线BF是⊙O的切线;
(2)若点D,点E分别是弧AB的三等分点,当AD=5时,求BF的长和扇形DOE的面积.
【答案】
(1)证明:∵∠CBF=∠CFB,
∴CB=CF,
又∵AC=CF,
∴CB= ![]() AF,
AF,
∴△ABF是直角三角形,
∴∠ABF=90°
∴直线BF是⊙O的切线
(2)解:连接DO,EO,
∵点D,点E分别是弧AB的三等分点,
∴∠AOD=60°,
又∵OA=OD,
∴△AOD是等边三角形,
∴∠OAD=60°,
又∵∠ABF=90°,AD=5,
∴AB=10,
∴BF=10 ![]() ;
;
扇形DOE的面积= ![]() =
= ![]() π.
π.

【解析】(1)证明直线BF是⊙O的切线,只需证明∠ABF=90°;(2)连接DO,EO,根据题意证明△AOD是等边三角形,得到△ABC是等边三角形,根据勾股定理求出BF的长,根据扇形面积公式: ![]() 求出扇形DOE的面积.
求出扇形DOE的面积.
【考点精析】本题主要考查了扇形面积计算公式的相关知识点,需要掌握在圆上,由两条半径和一段弧围成的图形叫做扇形;扇形面积S=π(R2-r2)才能正确解答此题.


 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:初中数学 来源: 题型:
【题目】如图(1),Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D。AF平分∠CAB,交CD于点E,交CB于点F。

(1)求证:CE=CF。
(2)将图(1)中的△ADE沿AB向右平移到△A′D′E′的位置,使点E′落在BC边上,其它条件不变,如图(2)所示。试猜想:BE′与CF有怎样的数量关系?请证明你的结论。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l与x轴,y轴分别交于M,N两点,且OM=ON=3.
(1)求这条直线的函数表达式;
(2)Rt△ABC与直线l在同一个平面直角坐标系内,其中∠ABC=90°,AC=2 ![]() ,A(1,0),B(3,0),将△ABC沿着x轴向左平移,当点C落在直线l上时,求线段AC扫过的面积.
,A(1,0),B(3,0),将△ABC沿着x轴向左平移,当点C落在直线l上时,求线段AC扫过的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小颖在教学楼四层楼上,每层楼高均为3米,测得目高1.5米,看到校园里的圆形花园最近点的俯角为60°,最远点的俯角为30°,请你帮小颖算出圆形花园的面积是多少平方米?(结果保留1位小数)
查看答案和解析>>
科目:初中数学 来源: 题型:
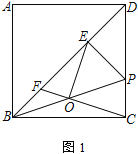
【题目】已知:在正方形ABCD中,AB=6,P为边CD上一点,过P点作PE⊥BD于点E,连接BP.
(1)O为BP的中点,连接CO并延长交BD于点F
①如图1,连接OE,求证:OE⊥OC;
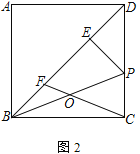
②如图2,若![]() ,求DP的长;
,求DP的长;
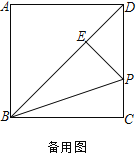
(2)![]() =___________
=___________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于点F,且AF=BD,连接BF.
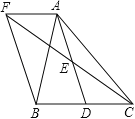
(1)BD与CD有什么数量关系,并说明理由;
(2)当△ABC满足什么条件时,四边形AFBD是矩形?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A,B,C,D四个点不在同一直线上,根据下列语句画图.
(1)画射线AB,画直线AC,画线段AD;
(2)连接BD与直线AC相交于点E;
(3)延长线段BC,反向延长线段DC;
(4)若在上述所画的图形中,设从点D到点C有四条路径,它们分别是①D→A→B→C;②D→B→C;③D→E→C;④D→C;哪条道路最短?并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)若关于x的方程2x﹣3=1和![]() =k﹣3x有相同的解,求k的值
=k﹣3x有相同的解,求k的值
(2)阅读材料:解方程组![]() 时,可由①得x﹣y=1③,然后再将③代入②得4×1﹣y=5,求得y=﹣1,从而进一步求得
时,可由①得x﹣y=1③,然后再将③代入②得4×1﹣y=5,求得y=﹣1,从而进一步求得![]() ,这种方法被称为“整体代入法”,请用上述方法解方程组
,这种方法被称为“整体代入法”,请用上述方法解方程组 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解不等式组 ![]() 请结合题意填空,完成本题的解答;
请结合题意填空,完成本题的解答;
(Ⅰ)解不等式①,得;
(Ⅱ)解不等式②,得;
(Ⅲ)把不等式①和②的解集在数轴上表示出来:
(Ⅳ)原不等式组的解集为 . ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com