
【题目】如图,在等腰梯形ABCD中,AD∥BC,AB=AD,BC=(![]() )AD, 以AD为边作等边三角形ADE,则∠BEC=______.
)AD, 以AD为边作等边三角形ADE,则∠BEC=______.
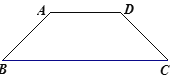
【答案】75°或165°
【解析】
过点A作AF∥CD交于F,可得四边形AFCD是平行四边形,根据平行四边形的性质得AD=FC,AF=CD,再求出BF,根据勾股定理逆定理判定△ABF是等腰直角三角形,再根据等腰直角三角形的性质求出∠ABF=45°,根据平行线的性质求出∠BAD=135°,然后分①点E在AD上方,根据周角等于360°求出∠BAE,根据等腰三角形的性质求出∠ABE,然后根据三角形的内角和定理列式计算即可得解;②点E在AD下方,求出∠BAE,再根据等腰三角形的性质求出∠ABE,然后求出∠CBE,再利用三角形的内角和列式计算即可.
在等腰梯形ABCD中,AB=CD,
过点A作AF∥CD交BC于F,
∵AD∥BC,
∴四边形AFCD是平行四边形,
∴AD=FC,AF=CD
∵AB=AD,BC=(![]() )AD,
)AD,
∴BF=BC-FC=(![]() )AD-AD=
)AD-AD=![]() AD,
AD,
在△ABF中,![]()
∴△ABF是等腰直角三角形,
∴∠ABF=45°
∵AD∥BC,
∴∠BAD=180°-∠ABF=135°
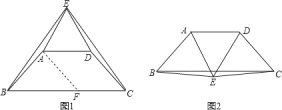
于是①如图1,等边三角形ADE的顶点E在AD的上方时,
∠BAE=360°-60°-135°=165°
∵AB=AD=AE,
∴∠ABE=![]() (180°-165°)=7.5°
(180°-165°)=7.5°
∴∠CBE=∠ABF+∠ABE=45°+7.5°=52.5°,
同理得∠BCE=52.5°
∴∠BEC=180°-52.5°×2=75°
另②如图2,等边三角形ADE的顶点E在AD的下方时,
∠BAE=∠BAD-∠DAE=135°-60°=75°
∵AB=AD=AE,
∴∠ABE=![]() (180°-75°)=52.5°
(180°-75°)=52.5°
∴∠CBE=∠ABE-∠ABC=45°+7.5°=7.5°,
∴∠BEC=180°-7.5°×2=165°
故答案为75°或165°


科目:初中数学 来源: 题型:
【题目】《九章算术》中记载:“今有共买羊,人出五,不足四十五;人出七,不足三,问人数、价价各几何?“其大意是:今有人合伙买羊,若每人出5钱,还差45钱;若每人出7钱,还差3钱,问:合伙人数、羊价各是多少?设合伙人数为![]() 人,羊价为
人,羊价为![]() 钱,根据题意,可列方程组( )
钱,根据题意,可列方程组( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
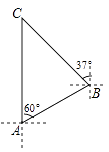
【题目】知识改变世界,科技改变生活.导航装备的不断更新极大方便了人们的出行.如图,某校组织学生乘车到黑龙滩(用C表示)开展社会实践活动,车到达A地后,发现C地恰好在A地的正北方向,且距离A地13千米,导航显示车辆应沿北偏东60°方向行驶至B地,再沿北偏西37°方向行驶一段距离才能到达C地,求B、C两地的距离.(参考数据:sin53°≈![]() ,cos53°≈
,cos53°≈![]() ,tan53°≈
,tan53°≈![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】.如图 1,B、D 分别是 x 轴和 y 轴的正半轴上的点,AD∥x 轴,AB∥y 轴(AD>AB),点 P 从 C 点出发,以 3cm/s 的速度沿 CDAB 匀速运动,运动到 B 点时终止;点 Q 从 B 点出发,以 2cm/s 的速度,沿 BCD 匀速运动,运动到 D 点时终止.P、Q 两点同时出发, 设运动的时间为 t(s),△PCQ 的面积为 S(cm2),S 与 t 之间的函数关系由图 2 中的曲线段 OE,线段 EF、FG 表示.
(1)求 AD 点的坐标;

(2)求图2中线段FG的函数关系式;
(3)是否存在这样的时间 t,使得△PCQ 为等腰三角形?若存在,直接写出 t 的值;若不存在, 请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
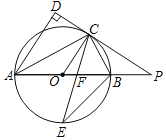
【题目】如图,已知AB是⊙O的直径,点C是⊙O上一点,AD与过点C的切线垂直,垂足为点D,直线DC与AB的延长线相交于点P,弦CE平分∠ACB,交AB于点F,连接BE.
(1)求证:AC平分∠DAB;
(2)求证:△PCF是等腰三角形;
(3)若AF=6,EF=2![]() ,求⊙O的半径长.
,求⊙O的半径长.
查看答案和解析>>
科目:初中数学 来源: 题型:
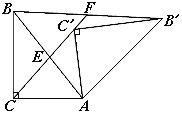
【题目】如图,Rt△ABC中,∠ACB=90°,Rt△AB′C′是由Rt△ABC绕点A顺时针旋转得到的,连接CC′交斜边于点E,CC′的延长线交BB′于点F.
(1)证明:△AC C′∽△AB B′;
(2)设∠ABC=α,∠CAC′=β,试探索α、β满足什么关系时AC=BF,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
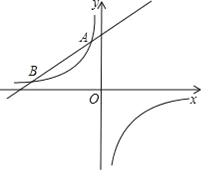
【题目】如图,一次函数y=kx+5(k为常数,且k≠0)的图象与反比例函数y=﹣8x-1的函数交于A(﹣2,b),B两点.
(1)求一次函数的表达式;
(2)若将直线AB向下平移m(m>0)个单位长度后与反比例函数的图象有且只有一个公共点,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
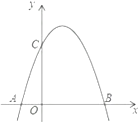
【题目】如图,是将抛物线y=-x2 平移后得到的抛物线,其对称轴为x=1,与x轴的一个交点为A(-1,0) ,另一交点为B,与y轴交点为C.
(1)求抛物线的函数表达式;
(2)若点N 为抛物线上一点,且BC⊥NC,求点N的坐标;
(3)点P是抛物线上一点,点Q是一次函数y=![]() x+
x+![]() 的图象上一点,若四边形OAPQ为平行四边形,这样的点P、Q是否存在?若存在,分别求出点P、Q的坐标,若不存在,说明理由.
的图象上一点,若四边形OAPQ为平行四边形,这样的点P、Q是否存在?若存在,分别求出点P、Q的坐标,若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一元二次方程x2+(2m+1)x+m2﹣1=0.
(1)若方程有两个不相等的实数根,试求m的取值范围;
(2)若抛物线y=x2+(2m+1)x+m2﹣1与直线y=x+m没有交点,试求m的取值范围;
(3)求证:不论m取何值,抛物线y=x2+(2m+1)x+m2﹣1图象的顶点都在一条定直线上.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com