
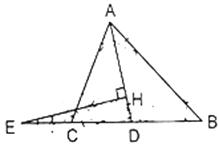
【题目】如图,![]() 是
是![]() 的角平分线,
的角平分线,![]() ,点
,点![]() 在
在![]() 延长线上且
延长线上且![]() 于
于![]() .
.
(1)若![]() ,求
,求![]() 的度数.
的度数.
(2)若![]() ,求
,求![]() 的度数.
的度数.
【答案】(1)105°;(2)20°.
【解析】
(1)根据三角形外角的性质可得∠ADC=75°,再根据垂直的定义可得∠EHD=∠AHE=90°,再根据三角形的内角和定理可求出∠E=15°,再根据三角形外角的性质即可得到![]() 的度数;
的度数;
(2)先根据三角形的内角和定理求出∠BAC的度数,再根据角平分线的性质求出∠CAD=25°,又因为![]() ,有∠AHE=90°,再利用三角形的外角及对顶角相等,可得∠E=∠ACB-(180°-∠AHE-∠CAD),把各角的度数代入即可求出∠E的度数.
,有∠AHE=90°,再利用三角形的外角及对顶角相等,可得∠E=∠ACB-(180°-∠AHE-∠CAD),把各角的度数代入即可求出∠E的度数.
解:∵![]() 是
是![]() 的角平分线,
的角平分线,
∴∠BAD=∠CAD=30°.
∵∠B=45°,
∴∠ADC=75°.
∵![]() ,
,
∴∠EHD=∠AHE=90°,
∴∠E=15°.
∵∠E+∠ACE=∠AHE+∠CAD,
∴∠ACE=90°+30°-15°=105°.
(2)∵∠BAC+∠B+∠ACB=180°, ![]() ,
,![]() ,
,
∴∠BAC=50°,
∵![]() 是
是![]() 的角平分线,
的角平分线,
∴∠CAD=![]() ∠BAC=25°,
∠BAC=25°,
∵∠E+∠ACE=∠CAD+∠AHE,
∴∠E=∠CAD+∠AHE-∠ACE
∵∠ACE=180°-∠ACB=95°,
∴∠E=25°+90°-95°=20°.


 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案科目:初中数学 来源: 题型:
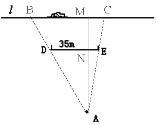
【题目】如示意图,小华家(点A处)和公路(l)之间竖立着一块35m长且平行于公路的巨型广告牌(DE).广告牌挡住了小华的视线,请在图中画出视点A的盲区,并将盲区内的那段公路计为BC.一辆以60km/h匀速行驶的汽车经过公路段的时间是3s,已知广告牌和公路的距离是40m,求小华家到公路的距离.(精确到1m)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】春平中学要为学校科技活动小组提供实验器材,计划购买A型、B型两种型号的放大镜.若购买8个A型放大镜和5个B型放大镜需用220元;若购买4个A型放大镜和6个B型放大镜需用152元.
(1)求每个A型放大镜和每个B型放大镜各多少元;
(2)春平中学决定购买A型放大镜和B型放大镜共75个,总费用不超过1180元,那么最多可以购买多少个A型放大镜?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】旅游公司在景区内配置了50辆观光车共游客租赁使用,假定每辆观光车一天内最多只能出租一次,且每辆车的日租金x(元)是5的倍数.发现每天的营运规律如下:当x不超过100元时,观光车能全部租出;当x超过100元时,每辆车的日租金每增加5元,租出去的观光车就会减少1辆.已知所有观光车每天的管理费是1100元.
(1)优惠活动期间,为使观光车全部租出且每天的净收入为正,则每辆车的日租金至少应为多少元?(注:净收入=租车收入﹣管理费)
(2)当每辆车的日租金为多少元时,每天的净收入最多?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明从家到学校上学,沿途需经过三个路口,每个路口都设有红、绿两种颜色的信号灯,在信号灯正常情况下:
(1)请用树状图列举小明遇到交通信号灯的所有情况;
(2)小明遇到两次绿色信号的概率有多大?
(3)小明红绿色两种信号都遇到的概率有多大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,AB为⊙O的直径,点C、D在⊙O上,且BC=6cm,AC=8cm,∠ABD=45°.

(1)求BD的长;
(2)求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有这样一个问题:探究函数y=-![]() +|x|的图象与性质.
+|x|的图象与性质.
小军根据学习函数的经验,对函数y=-![]() +|x|的图象与性质进行了探究.
+|x|的图象与性质进行了探究.
下面是小军的探究过程,请补充完整:
(1)函数y=-![]() +|x|的自变量x的取值范围是 ;
+|x|的自变量x的取值范围是 ;
(2)表是y与x的几组对应值.
x | -2 | -1.9 | -1.5 | -1 | -0.5 | 0 | 1 | 2 | 3 | 4 | … |
y | 2 | 1.60 | 0.80 | 0 | -0.72 | -1.41 | -0.37 | 0 | 0.76 | 1.55 | … |
在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点,根据描出的点,画出该函数的图象;

(3)观察图象,函数的最小值是 ;
(4)进一步探究,结合函数的图象,写出该函数的一条性质(函数最小值除外): .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(0,3)、B(3,4)、C(2,2)(正方形网格中每个小正方形的边长是一个单位长度).
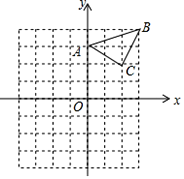
(1)△ABC向下平移4个单位长度得到的△A1B1C1,点C1的坐标是 ;
(2)以点B为位似中心,在网格内画出△A2B2C2,使△A2B2C2与△ABC位似,且位似比为2:1,点C2的坐标是 ;(画出图形)
(3)△A2B2C2的面积是 平方单位.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,四边形ABCD是平行四边形,AC、BD交于点O,∠1=∠2.
(1)求证:四边形ABCD是矩形;(2)若∠BOC=120°,AB=4cm,求四边形ABCD的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com