
【题目】如图,点O是△ABC内任一点,点D,E,F分别为OA,OB,OC的中点,则图中相似三角形有( )

A. 1对 B. 2对 C. 3对 D. 4对
【答案】D
【解析】
根据点D,E,F分别为OA,OB,OC的中点,可得DE是△AOB的中位线,DF是△AOC的中位线,EF是△BOC的中位线,可得DE//AB,DF//AC,EF//BC,进而可判定△DOE∽△AOD, △DOF∽△AOC, △EOF∽△BOC,根据中位线性质可得![]() ,
,![]() ,
,
继而可得![]() ,可判定△DEF∽△ABC.
,可判定△DEF∽△ABC.
因为点D,E,F分别为OA,OB,OC的中点,
所以DE是△AOB的中位线,DF是△AOC的中位线,EF是△BOC的中位线,
所以DE//AB,DF//AC,EF//BC,
所以△DOE∽△AOD, △DOF∽△AOC, △EOF∽△BOC,
因为DE是△AOB的中位线,DF是△AOC的中位线,EF是△BOC的中位线,
所以![]() ,
,![]() ,
,
所以![]() ,
,
所以△DEF∽△ABC,
因此有四对相似三角形,
故选D.


科目:初中数学 来源: 题型:
【题目】甲种污水处理器处理25吨的污水与乙种污水处理器处理35吨的污水所用的时间相同,已知乙种污水处理器每小时比甲种污水处理器多处理20吨的污水.
(1)分别求甲、乙两种污水处理器的污水处理效率;
(2)若某厂每天同时开甲、乙两种污水处理器处理污水共4小时,且甲、乙两种污水处理器处理污水每吨需要的费用分别30元和50元,问该厂每个月(以30天计)需要污水处理费多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,O是坐标原点,长方形OACB的顶点A、B分别在x轴与y轴上,已知OA=6,OB=10.点D为y轴上一点,其坐标为(0,2),点P从点A出发以每秒2个单位的速度沿线段AC﹣CB的方向运动,当点P与点B重合时停止运动,运动时间为t秒.
(1)当点P经过点C时,求直线DP的函数解析式;
(2)①求△OPD的面积S关于t的函数解析式;
②如图②,把长方形沿着OP折叠,点B的对应点B′恰好落在AC边上,求点P的坐标.
(3)点P在运动过程中是否存在使△BDP为等腰三角形?若存在,请求出点P的坐标;若不存在,请说明理由.



查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知AB=AC.如图,D、E为∠BAC的平分线上的两点,连接BD、CD、BE、CE;如图4, D、E、F为∠BAC的平分线上的三点,连接BD、CD、BE、CE、BF、CF;如图5, D、E、F、G为∠BAC的平分线上的四点,连接BD、CD、BE、CE、BF、CF、BG、CG……依此规律,第17个图形中有全等三角形的对数是( )

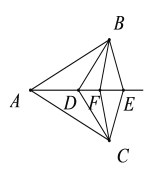

A.17B.54C.153D.171
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个铝质的三角形框架的三边长分别为24 cm,30 cm,36 cm,要做一个与它相似的铝质三角形的框架,现有长27 cm,45 cm的两根铝材,要求以其中的一根为边,从另一根上截下两段(允许有余材),则截法有______种.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC,按以下步骤作图:①分别以 B,C 为圆心,以大于![]() BC 的长为半径作弧,两弧相交于两点 M,N;②作直线 MN 交 AB 于点 D,连接 CD.若 CD=AC,∠A=50°,则∠ACB 的度数为
BC 的长为半径作弧,两弧相交于两点 M,N;②作直线 MN 交 AB 于点 D,连接 CD.若 CD=AC,∠A=50°,则∠ACB 的度数为
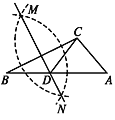
A.90°B.95°C.105°D.110°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解方程:
(1)(x-5)2=16 (直接开平方法) (2)x2+5x=0 (因式分解法)
(3)x2-4x+1=0 (配方法) (4)x2+3x-4=0 (公式法)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于x的一元二次方程(c+a)x2+2bx+(c-a)=0,其中a、b、c分别为△ABC三边的长.
(1)如果方程有两个相等的实数根,试判断△ABC的形状并说明理由;
(2)已知a:b:c=3:4:5,求该一元二次方程的根.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com