
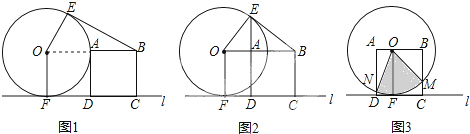
| OA |
| 2 |
| 2 |
| OA+2 |
| nπ |
| 90 |
| 2 |
| 3 |
| 2 |
| 3 |

| OA |
| OE |
| OE |
| OB |
| OA |
| 2 |
| 2 |
| OA+2 |
| 5 |
| n•π•22 |
| 360 |
| nπ |
| 90 |
| 90•π |
| 90 |
| 60π |
| 90 |
| 2 |
| 3 |
| 2 |
| 3 |


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
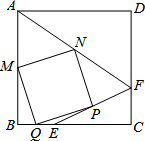 如图,在正方形ABCD中,E,F分别在BC,CD上,且BE=CF,M,N,P,Q分别是AB,AF,EF,BE的中点,判断四边形MNPQ的形状,并证明.
如图,在正方形ABCD中,E,F分别在BC,CD上,且BE=CF,M,N,P,Q分别是AB,AF,EF,BE的中点,判断四边形MNPQ的形状,并证明.查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图反映的是甲、乙两人以每分钟80米的速度从公司出发步行到火车站乘车的过程.在去火车站的途中,甲突然发现忘带预购的火车票,于是立刻以同样的速度返回公司,然后乘出租车赶往火车站,途中与乙相遇后,带上乙一同到火车站(忽略停顿所需时间),结果到火车站的时间比预计步行到火车站的时间早到了3分钟.
如图反映的是甲、乙两人以每分钟80米的速度从公司出发步行到火车站乘车的过程.在去火车站的途中,甲突然发现忘带预购的火车票,于是立刻以同样的速度返回公司,然后乘出租车赶往火车站,途中与乙相遇后,带上乙一同到火车站(忽略停顿所需时间),结果到火车站的时间比预计步行到火车站的时间早到了3分钟.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com