解:(1)①又∵△AOB和△COD都为等边三角形,
∴∠AOB=∠COD=60°,OA=OB,OC=OD,
∴∠AOB+∠BOC=∠COD+∠BOC,
即∠AOC=∠BOD,
在△AOC和△BOD中,
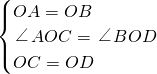
,
∴△AOC≌△BOD(SAS),
∴AC=BD;
②由△AOC≌△BOD,得∠OAC=∠OBD,
又∠AEO=∠PEB,∠APB=180°-(∠BEP+∠OBD),
∠AOB=180°-(∠OAC+∠AEO),
∴∠APB=∠AOB=60°;

(2)∵∠AOB=∠COD=α,
∴∠AOB+∠BOC=∠COD+∠BOC,
即∠AOC=∠BOD,
又∵△AOB和△COD都为等腰三角形,
∴OA=OB,OC=OD,
在△AOC和△BOD中,
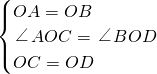
,
∴△AOC≌△BOD(SAS),
∴AC=BD;
由△AOC≌△BOD,得∠OAC=∠OBD,
又∠AEO=∠PEB,∠APB=180°-(∠BEP+∠OBD),
∠AOB=180°-(∠OAC+∠AEO),
∴∠APB=∠AOB=α;
(3)∵∠AOB=∠COD=α,
∴∠AOB+∠BOC=∠COD+∠BOC,
即∠AOC=∠BOD,
又OA=k•OB,OC=k•OD,
∴
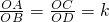
,
∴△OAC∽△OBD,
∴

,即AC=k•BD
∴∠ACO=∠BDO,
又∠OED=∠PEC,
∴∠DPC=∠COD=α,
则∠APB=180°-α.
故答案为:(2)AC=BD,α;(3)AC=k•BD,180°-α
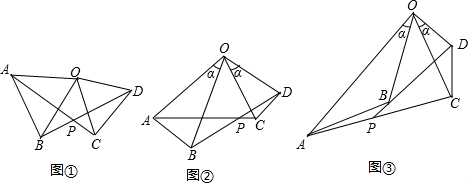
分析:(1)分析结论AC=BD可知,需要证明△AOC≌△BOD,围绕这个目标找全等的条件,由△AOB和△COD都是等边三角形,可得OA=OB,OD=OC,且∠AOB=∠COD=60°等号两边同时加上∠BOC,可得∠AOC=∠BOD,然后利用SAS可得△AOC≌△BOD,根据全等三角形的对应边相等得证;
(2)与图①比较,图形条件发生了变化,仍然可以证明△AOC≌△BOD,方法类似;
(3)由∠AOB=∠COD可得∠AOC=∠BOD,再由OA=k•OB,OC=k•OD,可得两边对应成比例,利用两边对应成比例且夹角相等的两三角形相似,可得△AOC∽△BOD,根据相似三角形的对应边成比例可得AC=k•BD,同时根据相似三角形的对应角相等可得∠ACO=∠BDO,再由一对对顶角相等,利用三角形的内角和定理可得∠DPC=∠COD=α,最后根据邻补角定义可表示出∠APB的度数.
点评:三角形全等的判定是中考的热点,一般以考查三角形全等的方法为主,判定两个三角形全等,先根据已知条件或求证的结论确定三角形,然后再根据三角形全等的判定方法,看缺什么条件,再去证什么条件.

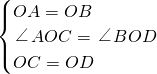 ,
,
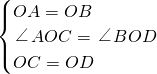 ,
,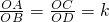 ,
, ,即AC=k•BD
,即AC=k•BD

 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案 ,测得C在B的北偏西45°方向上.
,测得C在B的北偏西45°方向上. 11、已知,如图,正比例函数与反比例函数的图象相交于A、B两点,A点坐标为(2,1),分别以A、B为圆心的圆与x轴相切,则图中两个阴影部分面积的和为
11、已知,如图,正比例函数与反比例函数的图象相交于A、B两点,A点坐标为(2,1),分别以A、B为圆心的圆与x轴相切,则图中两个阴影部分面积的和为 已知,如图,直角坐标系内的矩形ABCD,顶点A的坐标为(0,3),BC=2AB,P为
已知,如图,直角坐标系内的矩形ABCD,顶点A的坐标为(0,3),BC=2AB,P为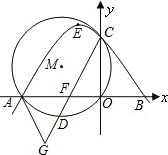 于C点,⊙M经过原点O及点A、C,点D是劣弧
于C点,⊙M经过原点O及点A、C,点D是劣弧