
【题目】如图,过抛物线y= ![]() x2﹣2x上一点A作x轴的平行线,交抛物线于另一点B,交y轴于点C,已知点A的横坐标为﹣2.
x2﹣2x上一点A作x轴的平行线,交抛物线于另一点B,交y轴于点C,已知点A的横坐标为﹣2.
(1)求抛物线的对称轴和点B的坐标;
(2)在AB上任取一点P,连结OP,作点C关于直线OP的对称点D;
①连结BD,求BD的最小值;
②当点D落在抛物线的对称轴上,且在x轴上方时,求直线PD的函数表达式.
【答案】
(1)
解:由题意A(﹣2,5),对称轴x=﹣ ![]() =4,
=4,
∵A、B关于对称轴对称,
∴B(10,5).
(2)
解:①如图1中,
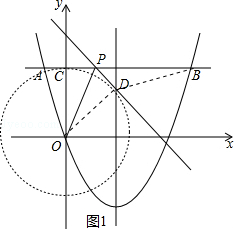
由题意点D在以O为圆心OC为半径的圆上,
∴当O、D、B共线时,BD的最小值=OB﹣OD= ![]() ﹣5=5
﹣5=5 ![]() ﹣5.
﹣5.
②如图中,

当点D在对称轴上时,在Rt△ODE中,OD=OC=5,OE=4,
∴DE= ![]() =
= ![]() =3,
=3,
∴点D的坐标为(4,3).
设PC=PD=x,在Rt△PDK中,x2=(4﹣x)2+22,
∴x= ![]() ,
,
∴P( ![]() ,5),
,5),
∴直线PD的解析式为y=﹣ ![]() x+
x+ ![]() .
.
【解析】(1)思想确定点A的坐标,利用对称轴公式求出对称轴,再根据对称性可得点B坐标;(2)①由题意点D在以O为圆心OC为半径的圆上,推出当O、D、B共线时,BD的最小值=OB﹣OD;②当点D在对称轴上时,在Rt△OD=OC=5,OE=4,可得DE= ![]() =
= ![]() =3,求出P、D的坐标即可解决问题;
=3,求出P、D的坐标即可解决问题;
【考点精析】通过灵活运用抛物线与坐标轴的交点,掌握一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.即可以解答此题.


科目:初中数学 来源: 题型:
【题目】已知抛物线y=x2-2x-3与x轴相交于A、B两点,其顶点为M,将此抛物线在x轴下方的部分沿x轴翻折,其余部分保持不变,得到一个新的图象.如图,当直线y=-x+n与此图象有且只有两个公共点时,则n的取值范围为 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店销售10台A型和20台B型电脑的利润为4000元,销售20台A型和10台B型电脑的利润为3500元.
(1)求每台A型电脑和B型电脑的销售利润;
(2)该商店计划一次购进两种型号的电脑共100台,其中B型电脑的进货量不超过A型电脑的2倍,设购进A型电脑x台,这100台电脑的销售总利润为y元. ①求y关于x的函数关系式;
②该商店购进A型、B型电脑各多少台,才能使销售总利润最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】股民李星星在上周星期五以每股 11.2 元买了一批股票,下表为本周星期一 到星期五该股票的涨跌情况

求:(1)本周星期三收盘时,每股的钱数.
(2)李星星本周内哪一天把股票抛出比较合算,为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以平行四边形ABCD的边CD为斜边向内作等腰直角△CDE,使AD=DE=CE,∠DEC=90°,且点E在平行四边形内部,连接AE、BE,则∠AEB的度数是( )
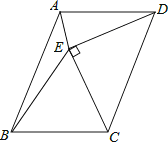
A、120° B、135° C、150° D、45°
查看答案和解析>>
科目:初中数学 来源: 题型:
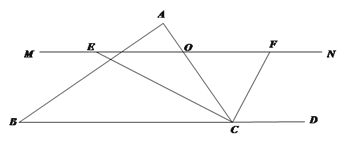
【题目】已知△ABC中,点O是边AC上的一个动点,过O作直线MN∥BC,设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F.
(1)求证:OE=OF.
(2)试确定点O在边AC上的位置,使四边形AECF是矩形,并加以证明.
(3)在(2)的条件下,且△ABC满足 ____________时,矩形AECF是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,用火柴棒按下列方式搭三角形:

(1)填写下面表
三角形个数 | 1 | 2 | 3 | 4 | … |
火柴棒根数 | … |
(2)搭10个这样的三角形需要 根火柴棒.
(3)搭n个这样的三角形需要 根火柴棒.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,AB是⊙O的直径,点C在⊙O上,过点C的直线与AB的延长线交于点P. 
(1)如图①,若∠COB=2∠PCB,求证:直线PC是⊙O的切线;
(2)如图②,若点M是AB的中点,CM交AB于点N,MNMC=36,求BM的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com