
分析 设P(x,y)为圆上一点,则有(x-1)2+(y-1)2=r2,由$\left\{\begin{array}{l}{(x-1)^{2}+(y-1)^{2}={r}^{2}}\\{y=kx+(1-3k)}\end{array}\right.$,消去y得到,(k2+1)x2-(2+6k2)x+9k2+1-r2=0,因为△=(2+6k2)2-4(k2+1)(9k2+1-r2)=4k2(r2-16)+4r2,由题意r2>16时,可保证不论k为何值,经过的船只总有一段路径会被监测到,解不等式即可.
解答 解:设P(x,y)为圆上一点,则有(x-1)2+(y-1)2=r2,
由$\left\{\begin{array}{l}{(x-1)^{2}+(y-1)^{2}={r}^{2}}\\{y=kx+(1-3k)}\end{array}\right.$,
消去y得到,(k2+1)x2-(2+6k2)x+9k2+1-r2=0,
∵△=(2+6k2)2-4(k2+1)(9k2+1-r2)=4k2(r2-16)+4r2,
由题意r2>16时,可保证不论k为何值,经过的船只总有一段路径会被监测到.
∴r>4时,可保证不论k为何值,经过的船只总有一段路径会被监测到.
故答案为r>4.
点评 本题考查一次函数的应用、方程组、一元二次方程的根判别式等知识,解题的关键是灵活运用所学知识解决问题,题目比较难,属于中考填空题中的压轴题.


 应用题作业本系列答案
应用题作业本系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
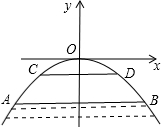 如图,有一座抛物线形拱桥,在正常水位时水面AB的宽为20m,如果水位上升3m水面CD的宽是10m.
如图,有一座抛物线形拱桥,在正常水位时水面AB的宽为20m,如果水位上升3m水面CD的宽是10m.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 甲、乙两地相距300千米,一辆货车和一辆轿车先后从甲地出发向乙地,轿车比货车晚出发1.5小时,如图,线段OA表示货车离甲地距离y(千米)与时间x(小时)之间的函数关系;折线BCD表示轿车离甲地距离y(千米)与时间x(时)之间的函数关系,请根据图象解答下列问题:
甲、乙两地相距300千米,一辆货车和一辆轿车先后从甲地出发向乙地,轿车比货车晚出发1.5小时,如图,线段OA表示货车离甲地距离y(千米)与时间x(小时)之间的函数关系;折线BCD表示轿车离甲地距离y(千米)与时间x(时)之间的函数关系,请根据图象解答下列问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com