
【题目】如图,在△ABC中,点B,C是x轴上的两个定点,∠ACB=90°,AC=BC,点A(l,3),点P是x轴上的一个动点,点E是AB的中点,在△PEF中,∠PEF=90°,PE=EF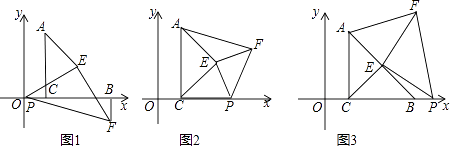
(1)如图1,当点P与坐标原点重合时:①求证△PCE≌△FBE;②求点F的坐标;
(2)如图2,当点P在线段CB上时,求证S△CPE=S△AEF
(3)如图3,当点P在线段CB的延长线时,若S△AEF=4S△PBE则此刻点F的坐标为
【答案】
(1)
证明:如图1中,

①∵A(1,3),B(4,0),
∴AC=BC=3,△ACB是等腰直角三角形,
∵AE=EB,
∴CE=AE=EB,CE⊥AB,∠ECB=∠EBC=45°,
∴∠CEB=∠OEF=90°,∠ECO=135°,
∴∠OEC=∠FEB,∵OE=EF,EC=EB,
∴△EOC≌△EFB,即△PCE≌△FBE..
②∵△PCE≌△FBE.
∴OC=BF=1,∠EBF=∠OCE=135°,
∴∠OBF=90°,
∴BF⊥OB,
∴F(4,﹣1)
(2)
证明:如图2中,作PM⊥CE于M,FN⊥EB于N.

由(1)可知∠OEC=∠FEB,OE=EF,EC=EB,
∴△ECP≌△EBF,
∵PM⊥CE于M,FN⊥EB于N,
∴PM=FN(全等三角形对应边上的高相等),
∵S△CPE= ![]() CEPM,S△AEF=
CEPM,S△AEF= ![]() AEFN,
AEFN,
∵CE=AE,PM=NF,
∴S△CPE=S△AEF
(3)(4,4)
【解析】(3)解:如图3中,
由(2)可知△ECP≌△EBF,推出PC=BF,BF⊥CP,
∵S△CPE=S△AEF , S△AEF=4S△PBE ,
∴S△CPE=4S△PBE ,
∴PC=4PB,
∴BC=3PB,PB=1,PC=4,
∴BF=PC=4,
∴点F坐标为(4,4).
所以答案是(4,4).
【考点精析】解答此题的关键在于理解全等三角形的性质的相关知识,掌握全等三角形的对应边相等; 全等三角形的对应角相等.


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:初中数学 来源: 题型:
【题目】计算(-3xy2)·(2y2-xyz+1)的结果是( )
A. -3xy4+32y3+3xy2 B. -6xy4+3x2y3z-3xy2
C. -6xy4-3x2y3z-3xy2 D. -6xy4+3x2y2z
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2-8ax(a<0)的图像与x轴的正半轴交于点A,它的顶点为P.点C为y轴正半轴上一点,直线AC与该图像的另一交点为B,与过点P且垂直于x轴的直线交于点D,且CB:AB=1:7.
(1)求点A的坐标及点C的坐标(用含a的代数式表示);
(2)连接BP,若△BDP与△AOC相似(点O为原点),求此二次函数的关系式.

查看答案和解析>>
科目:初中数学 来源: 题型:
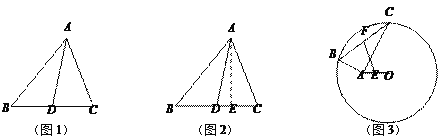
【题目】阅读理解:小明热爱数学,在课外书上看到了一个有趣的定理——“中线长定理”:三角形两边的平方和等于第三边的一半与第三边上的中线的平方和的两倍.如图1,在△ABC中,点D为BC的中点,根据“中线长定理”,可得:
AB2+AC2=2AD2+2BD2.
小明尝试对它进行证明,部分过程如下:
解:过点A作AE⊥BC于点E,如图2,在Rt△ABE中,AB2=AE2+BE2,
同理可得:AC2=AE2+CE2,AD2=AE2+DE2,
为证明的方便,不妨设BD=CD=x,DE=y,
∴AB2+AC2=AE2+BE2+AE2+CE2=……
(1)请你完成小明剩余的证明过程;
理解运用:
(2) ① 在△ABC中,点D为BC的中点,AB=6,AC=4,BC=8,则AD=_______;
② 如图3,⊙O的半径为6,点A在圆内,且OA=2![]() ,点B和点C在⊙O上,且∠BAC=90°,点E、F分别为AO、BC的中点,则EF的长为________;
,点B和点C在⊙O上,且∠BAC=90°,点E、F分别为AO、BC的中点,则EF的长为________;
拓展延伸:
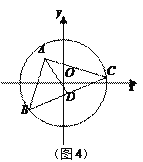
(3)小明解决上述问题后,联想到《能力训练》上的题目:如图4,已知⊙O的半径为5![]() ,以A(3,4)为直角顶点的△ABC的另两个顶点B,C都在⊙O上,D为BC的中点,求AD长的最大值.请你利用上面的方法和结论,求出AD长的最大值.
,以A(3,4)为直角顶点的△ABC的另两个顶点B,C都在⊙O上,D为BC的中点,求AD长的最大值.请你利用上面的方法和结论,求出AD长的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列多项式的乘法中,能用平方差公式计算的是( )
A.(-m +n)(m - n)
B.( ![]() a +b)(b -
a +b)(b - ![]() a)
a)
C.(x + 5)(x + 5)
D.(3a -4b)(3b +4a)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一张足够大的纸板上截取一个面积为3600平方厘米的矩形纸板ABCD,如图1,再在矩形纸板的四个角上切去边长相等的小正方形,再把它的边沿虚线折起,做成一个无盖的长方体纸盒,底面为矩形EFGH,如图2.设小正方形的边长为x厘米.
(1)当矩形纸板ABCD的一边长为90厘米时,求纸盒的侧面积的最大值;
(2)当EH:EF=7:2,且侧面积与底面积之比为9:7时,求x的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某招聘考试分笔试和面试两种,其中笔试按60%、面试按40%计算加权平均数,作为总成绩.孔明笔试成绩90分,面试成绩85分,那么孔明的总成绩是 分.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com