
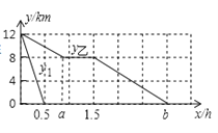
����Ŀ����ͼ��1����A1B1��A2B2��ˮ�������ڵ�����������������������ƽ�е��߶Σ�������һ����Ӿ�˶�����������һ����Ӿ�����ߣ���������A1B1�ϴ�A1������������B1����ͬ�����ٶȷ���A1����Ȼ���ظ��������̣���������A2B2����1.5m/s���ٶȴ�B2������������A2������ͬ���ٶȻص�B2����Ȼ���ظ��������̣�������ÿ���۷�ʱ�ļ��ٺ�ת��ʱ�䣩�����ס�������ͬʱ���������뿪�ر�B1B2�ľ���Ϊy��m�����˶�ʱ��Ϊt��s�������ζ�ʱ��y��m����t��s���ĺ���ͼ����ͼ��2����ʾ��
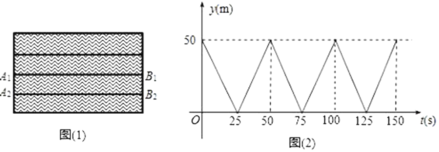
��1�������ij������� m�����ٶ����� m/s����t=�� ��sʱ���ס������˵�һ����������t=�� ��sʱ���ס������˵ڶ���������
��2������������ʱ�����˾�ر�B1B2�����ף�
���𰸡���1��50��2��![]() ��
��![]() ����2��
����2��![]()
��������
��1���ɺ���ͼ�����ֱ�ӵó������ij���Ϊ50�ף���·����ʱ��=�ٶȾͿ���������ٶȣ��辭��x��ʱ���ס������˵ڶ������������ݼ��ι���·��+���ι���·�̣��������������⼴�ɣ�
��2�����ٶ���ʱ��Ĺ�ϵ�Ϳ���������ۣ�
�⣺��1����ͼ�������ij����ǣ�50�ף�
���ٶ��ǣ�50��25=2m/s��
�辭��x��ʱ���ס������˵�һ�������������⣬2x+1.5x=50��
��x=![]() ��
��
�辭��x��ʱ���ס������˵ڶ��������������⣬��
2x+1.5x=150��
��ã�x=![]() ��
��
�ʴ�Ϊ��50��2��![]() ��
��![]() ��
��
��2���辭��x s�����˵�������������1��5+2��x=250 ��x=![]() ��
��
�����������ʱ�����˾�ر�B1B 2 ��150��![]() ��2=
��2=![]() m��
m��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪![]() ��
��![]() ����
����![]() �ķ���
�ķ���![]() ������ʵ����.
������ʵ����.
��1����![]() ʱ����
ʱ����![]() ��ֵ��
��ֵ��
��2��������![]() ��һ�߳�
��һ�߳�![]() �������߳�Ϊ
�������߳�Ϊ![]() ��
��![]() ����
����![]() ���ܳ�.
���ܳ�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪������ABCD�ı߳�Ϊ8����E���������ڲ�һ�㣬����BE��CE���ҡ�ABE����BCE����P��AB����һ���㣬����PD��PE����PD+PE�ij�����СֵΪ_____��
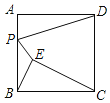
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��AOB��60����OC�ǡ�AOB��ƽ���ߣ���DΪOC��һ�㣬��D��ֱ��DE��OA������Ϊ��E����ֱ��DE��OB�ڵ�F����ͼ��ʾ����DE��2����DF��_____��
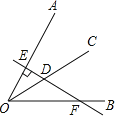
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1�����㣺��![]() ��1��0+2sin30��-
��1��0+2sin30��-![]() +|��2017|��
+|��2017|��
��2����ͼ������ABC�У���֪��ABC=30��������ABC�Ƶ�B��ʱ����ת50����õ���A1BC1������A=100������֤��A1C1��BC��
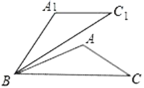
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ڷ���������y=��![]() ������˵����ȷ���ǣ�������
������˵����ȷ���ǣ�������
A.ͼ���ڵ�һ��������B.ͼ���㣨2����8��
C.��x��0ʱ��y��x���������СD.��x��0ʱ��y��x�����������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�����ڴӼص��ҵص�·����![]() ��С�����дӼص��ҵ����棬�ٶ�Ϊ
��С�����дӼص��ҵ����棬�ٶ�Ϊ![]() ������
������![]() ����;��Ϣ��һ��ʱ�䣬Ȼ�������ԭ��ǰ���ҵأ������Ӽؿ����ҵصĵ�ƿ��ÿ����Сʱ��һ�˳����ٶ���
����;��Ϣ��һ��ʱ�䣬Ȼ�������ԭ��ǰ���ҵأ������Ӽؿ����ҵصĵ�ƿ��ÿ����Сʱ��һ�˳����ٶ���![]() ����С�����1�˵�ƿ��ͬʱ��������С�����ҵص�·��Ϊ
����С�����1�˵�ƿ��ͬʱ��������С�����ҵص�·��Ϊ![]() ����
����![]() �˵�ƿ�����ҵص�·��Ϊ
�˵�ƿ�����ҵص�·��Ϊ![]() ��
��![]() Ϊ���������н�ʱ��Ϊ
Ϊ���������н�ʱ��Ϊ![]() .��ͼ������
.��ͼ������![]() ��
��![]() ��
��![]() �ĺ���ͼ��
�ĺ���ͼ��
��1���۲�ͼ������![]() ��
��![]() ��
��
��2�����2�˵�ƿ�����ҵص�·��![]() ��
��![]() �ĺ�����ϵʽ��
�ĺ�����ϵʽ��
��3����![]() ʱ����ͼ�л���
ʱ����ͼ�л���![]() ��
��![]() �ĺ���ͼ���۲�ͼ�ó�С������Ϣ��ǰ���ҵص�;�У����� �˵�ƿ��ʻ����
�ĺ���ͼ���۲�ͼ�ó�С������Ϣ��ǰ���ҵص�;�У����� �˵�ƿ��ʻ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���ABCD�У�AB=4��BC=10��PΪ����AB��һ�㣬����PD��AC����PD��AC���ڵ�E������A��AF��PD������Ϊ��F��
(1)����F����BC����ʱ����AP��ֵ
(2)����PAEΪ����������ʱ����AP��ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
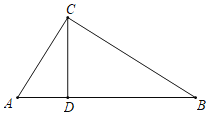
����Ŀ����ͼ����Rt��ABC�У���ACB��90�㣬CD��AB��D��AC��![]() ��BD��4��
��BD��4��
��1����֤����ACD�ס�ABC��
��2�����ABC�������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com