练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图,⊙O为△ABC的内切圆,D、E、F为切点,∠DOB="73°,∠DOE=120°," 则∠DOF=_______度,∠C=______度,∠A=_______度.

     

    【答案】

    146°,60°,86°

    【解析】

    试题分析：根据切线的性质结合四边形内角和定理即可求得结果.

    ∵⊙O为△ABC的内切圆，∠DOB=73°,∠DOE=120°

    ∴∠DOF=146°，∠C=60°

    ∴∠EOF=94°

    ∴∠A=86°.

    考点：切线的性质，四边形内角和定理

    点评：切线的性质是圆中非常重要的知识点，是中考的热点，在各种题型中均有出现，一般难度不大，需多加注意.

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    25、已知：如图AD为△ABC的高，E为AC上一点，BE交AD于F，且有BF=AC，FD=CD，求证：BE⊥AC．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

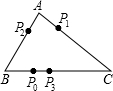    精英家教网电子跳蚤游戏盘（如图）为△ABC，AB=8，AC=9，BC=10，如果电子跳蚤开始时在BC边一的P0点，BP0=4．第一步跳蚤跳到AC边上P1点，且CP1=CP0；第二步跳蚤从P1跳到AB边上P2点，且AP2=AP1；第三步跳蚤从P2 跳回到BC边上P3点，且BP3=BP2；…跳蚤按上述规则跳下去，第2003次落点为P2003，则P3与P2003之间的距离为
     
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图G为△ABC的重心，GE∥AC，若S△ABC=36，则S△GDE=
    2
    2
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    精英家教网已知如图AD为△ABC上的高，E为AC上一点BE交AD于F且有BF=AC，FD=CD，要证明△ADC≌△BDF需要的判断方法是（　　）
    A、HLB、SSSC、SASD、ASA

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    已知如图AD为△ABC上的高，E为AC上一点BE交AD于F且有BF=AC，FD=CD．
    求证：∠C=∠AFE．

    查看答案和解析>>

    同步练习册答案