

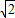
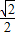
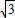
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:初中数学 来源: 题型:
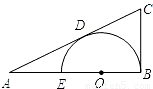
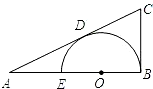 如图,CA,CB分别与⊙O相切于点D,B,圆心O在AB上,AB与⊙O的另一交点为E,AE=2,⊙O的半径为1,则BC的长为( )
如图,CA,CB分别与⊙O相切于点D,B,圆心O在AB上,AB与⊙O的另一交点为E,AE=2,⊙O的半径为1,则BC的长为( )A、
| ||||
B、2
| ||||
C、
| ||||
D、
|
查看答案和解析>>
科目:初中数学 来源:第24章《圆(下)》中考题集(05):24.2 圆的切线(解析版) 题型:选择题
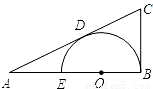
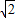
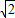
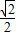
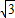
查看答案和解析>>
科目:初中数学 来源:第28章《圆》中考题集(28):28.2 与圆有关的位置关系(解析版) 题型:选择题
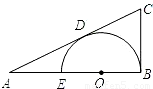
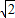
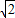
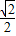

查看答案和解析>>
科目:初中数学 来源:第24章《圆》中考题集(22):24.2 点、直线和圆的位置关系(解析版) 题型:选择题


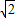
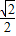
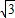
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com