
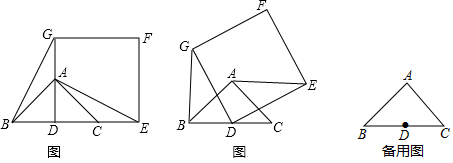
分析 (1)在Rt△BDG与Rt△EDA;根据边角边定理易得Rt△BDG≌Rt△EDA;故BG=AE;
(2)连接AD,根据直角三角形与正方形的性质可得Rt△BDG≌Rt△EDA;进而可得BG=AE;
(3)根据(2)的结论,求BG的最大值,分析可得此时F的位置,由勾股定理可得答案.
解答 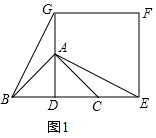 (1)证明:∵△ABC是等腰直角三角形,∠BAC=90°,点D是BC的中点,
(1)证明:∵△ABC是等腰直角三角形,∠BAC=90°,点D是BC的中点,
∴AD⊥BC,BD=CD,
∴∠ADB=∠ADC=90°,AD=DC=DB,
∵四边形DEFG是正方形,
∴DE=DG,
∴△ADE≌△BDG(SAS),
∴BG=AE;
(2)成立;
理由如下:如图2,连接AD,
由(1)知AD=BD,AD⊥BC.
∴∠ADG+∠GDB=90°.
∵四边形EFGD为正方形,
∴DE=DG,且∠GDE=90°.
∴∠ADG+∠ADE=90°
∴∠BDG=∠ADE.
在△BDG和△ADE中,
∵BD=AD,∠BDG=∠ADE,GD=ED,
∴△BDG≌△ADE(SAS)
∴AE=BG;
(3)α=270°;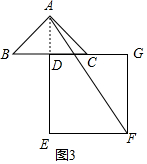
正方形DEFG如图3所示
由(2)知BG=AE
∴当BG取得最大值时,AE取得最大值.
∵BC=DE=4,
∴EF=4,
∴BG=2+4=6
∴AE=6
在Rt△AEF中,由勾股定理,得
AF=$\sqrt{A{E}^{2}+E{F}^{2}}$=$\sqrt{36+16}$=2$\sqrt{13}$.
点评 解答本题要充分利用正方形的特殊性质.注意在正方形中的特殊三角形的应用,搞清楚矩形、菱形、正方形中的三角形的三边关系,可有助于提高解题速度和准确率.


 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:初中数学 来源: 题型:选择题
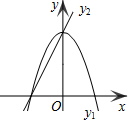 如图,已知抛物线y1=-2x2+2,直线y2=2x+2,当x任取一值时,x对应的函数值分别为y1、y2.若y1≠y2,取y1、y2中的较小值记为M;若y1=y2,记M=y1=y2.例如:当x=1时,y1=0,y2=4,y1<y2,此时M=0.下列判断:
如图,已知抛物线y1=-2x2+2,直线y2=2x+2,当x任取一值时,x对应的函数值分别为y1、y2.若y1≠y2,取y1、y2中的较小值记为M;若y1=y2,记M=y1=y2.例如:当x=1时,y1=0,y2=4,y1<y2,此时M=0.下列判断:| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
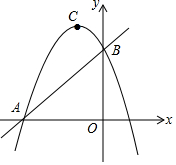 如图,直线y=x+n与x轴交于点A,与y轴交于点B(点A与点B不重合),抛物线y=-$\frac{1}{2}$x2-2x+c经过点A、B,抛物线的顶点为C.
如图,直线y=x+n与x轴交于点A,与y轴交于点B(点A与点B不重合),抛物线y=-$\frac{1}{2}$x2-2x+c经过点A、B,抛物线的顶点为C.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0.6与0.7之间 | B. | 0.7与0.8之间 | C. | 0.8与0.9之间 | D. | 0.9与1之间 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com