
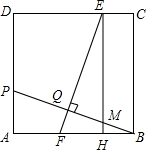
 如图,在正方形ABCD中,点P在AD上,且不与A、D重合,BP的垂直平分线分别交CD、AB于E、F两点,垂足为Q,过E作EH⊥AB于H.
如图,在正方形ABCD中,点P在AD上,且不与A、D重合,BP的垂直平分线分别交CD、AB于E、F两点,垂足为Q,过E作EH⊥AB于H.分析 (1)先根据EQ⊥BP,EH⊥AB得出∠EQN=∠BHM=90°.根据∠EMQ=∠BMH得出△EMQ∽△BMH,故∠QEM=∠HBM.由ASA定理得出△APB≌△HFE,故可得出结论;
(2)由勾股定理求出BP的长,根据EF是BP的垂直平分线可知BQ=$\frac{1}{2}$BP,再根据锐角三角函数的定义得出QF=BQ的长,由(1)知,△APB≌△HFE,故EF=BP=4$\sqrt{10}$,再根据EQ=EF-QF即可得出结论.
解答 (1)证明:∵EQ⊥BP,EH⊥AB,
∴∠EQN=∠BHM=90°.
∵∠EMQ=∠BMH,
∴△EMQ∽△BMH,
∴∠QEM=∠HBM.
在Rt△APB与Rt△HFE中,
$\left\{\begin{array}{l}∠PAB=∠FHE\\ AB=EH\end{array}\right.$,
∴△APB≌△HFE,
∴HF=AP;
(2)解:由勾股定理得,BP=$\sqrt{{AP}^{2}+{AB}^{2}}$=$\sqrt{{4}^{2}+{12}^{2}}$=4$\sqrt{10}$.
∵EF是BP的垂直平分线,
∴BQ=$\frac{1}{2}$BP=2$\sqrt{10}$,
∴QF=BQ•tan∠FBQ=BQ•tan∠ABP=2$\sqrt{10}$×$\frac{4}{12}$=$\frac{2\sqrt{10}}{3}$.
由(1)知,△APB≌△HFE,
∴EF=BP=4$\sqrt{10}$,
∴EQ=EF-QF=4$\sqrt{10}$-$\frac{2\sqrt{10}}{3}$=$\frac{10\sqrt{10}}{3}$.
点评 本题考查的是正方形的性质,熟知正方形的性质及全等三角形的判定与性质是解答此题的关键.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
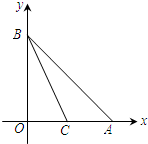 如图,点A和点B分别在x轴和y轴上,且OA=OB=4,直线BC交x轴于点C,S△BOC=S△ABC.
如图,点A和点B分别在x轴和y轴上,且OA=OB=4,直线BC交x轴于点C,S△BOC=S△ABC.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -5 | B. | -1 | C. | 1 | D. | 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知点O(0,0),B(2,3),点A在坐标轴上,且S△AOB=6.
已知点O(0,0),B(2,3),点A在坐标轴上,且S△AOB=6.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
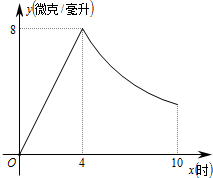 某药品研究所开发一种抗菌新药,经多年动物实验,首次用于临床人体实验.测得成人服药后血液中药物浓度y(微克/毫升)与服药时间x小时之间的函数关系如图所示(当4≤x≤10时,y与x成反比).
某药品研究所开发一种抗菌新药,经多年动物实验,首次用于临床人体实验.测得成人服药后血液中药物浓度y(微克/毫升)与服药时间x小时之间的函数关系如图所示(当4≤x≤10时,y与x成反比).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com