
| |||||||||||||||||||
(1) |
因为AB=AC,所以∠B=∠ACB,所以∠B= 又∠BNM=90°,所以∠NMB=90°-∠B=90°-70°=20°. |
(2) |
同理可求得∠NMB=35°. |
(3) |
猜想规律:等腰三角形一腰的垂直平分线与底边或底边的延长线的夹角等于顶角的一半,即∠NMB= 证明:设∠A=α. 因为AB=AC,所以∠B=∠C= 因为∠BNM=90°,所以∠NMB=90°-∠B=90°- |
(4) |
由(3)中的证明知:若将(1)中的∠A改为钝角,这个规律仍然成立,不必修改. |


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
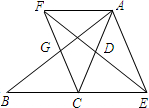 如图所示,在△ABC中,D是AC的中点,E是线段BC延长线上一点,过点A作AF∥BC交ED的延长线于点F,连接AE,CF.
如图所示,在△ABC中,D是AC的中点,E是线段BC延长线上一点,过点A作AF∥BC交ED的延长线于点F,连接AE,CF.查看答案和解析>>
科目:初中数学 来源: 题型:
 15、如图所示,在△ABC中,DM、EN分别垂直平分AB和AC,交BC于D、E,若∠DAE=50°,则∠BAC=
15、如图所示,在△ABC中,DM、EN分别垂直平分AB和AC,交BC于D、E,若∠DAE=50°,则∠BAC=查看答案和解析>>
科目:初中数学 来源: 题型:
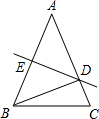 如图所示,在△ABC中,AB=AC,DE是边AB的垂直平分线,交AB于E,交AC于D,若△BCD的周长为18cm,△ABC的周长为30cm,那么BE的长为
如图所示,在△ABC中,AB=AC,DE是边AB的垂直平分线,交AB于E,交AC于D,若△BCD的周长为18cm,△ABC的周长为30cm,那么BE的长为查看答案和解析>>
科目:初中数学 来源: 题型:
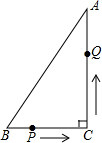 如图所示,在△ABC中,BC=7cm,AB=25cm,AC=24cm,P点在BC上从B点向C点运动(不包括点C),点P的运动速度为2cm∕s;Q点在AC上从C点向点A运动(不包括点A),运动速度为5cm∕s,若点P、Q分别从B、C同时运动,请解答下面的问题,并写出主要过程.
如图所示,在△ABC中,BC=7cm,AB=25cm,AC=24cm,P点在BC上从B点向C点运动(不包括点C),点P的运动速度为2cm∕s;Q点在AC上从C点向点A运动(不包括点A),运动速度为5cm∕s,若点P、Q分别从B、C同时运动,请解答下面的问题,并写出主要过程.| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com