
 如图,Rt△ABC中,∠C=90°,AD平分∠CAB,交CB于点D,DE垂直平分AB,DE=2cm.求BC的长.
如图,Rt△ABC中,∠C=90°,AD平分∠CAB,交CB于点D,DE垂直平分AB,DE=2cm.求BC的长. 分析 通过DE垂直平分AB于E,推出AD=BD,可得∠B=∠DAB,然后,由AD为∠CAB的角平分线,∠C=90°,根据三角形内角和定理,可知∠B=∠DAB=∠CAD=30°,同时也可推出,CD=DE,BD=2DE,由DE=2,即可推出BC的长度.
解答 解:∵DE垂直平分AB于E,
∴AD=BD,
∴∠B=∠DAB,
∵AD为∠CAB的角平分线,∠C=90°,
∴∠B=∠DAB=∠CAD,CD=DE,
∵∠B+∠CAB=90°,
∴∠B=30°,
∴BD=2DE,
∵DE=2cm,
∴CD=2cm,BD=4cm,
∴BC=6cm.
点评 本题主要考查角平分线的性质定理,线段的中垂线的性质定理,含30度角的直角三角形的相关性质,关键在于根据有关性质求出∠B的度数,推出BD=2DE,CD=DE.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
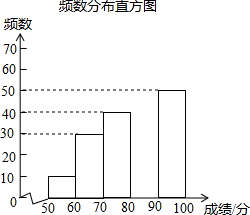 中华文明,源远流长:中华汉字,寓意深广,为了传承优秀传统文化,某校团委组织了一次全校1500名学生参加的“汉字听写”大赛,赛后发现所有参赛学生的成绩均不低于50分.为了更好地了解本次大赛的成绩分布情况,随机抽取了部分参赛学生的成绩作为样本进行处理,得到下列不完整的统计图表.请你根据表中提供的信息,解答下列问题:
中华文明,源远流长:中华汉字,寓意深广,为了传承优秀传统文化,某校团委组织了一次全校1500名学生参加的“汉字听写”大赛,赛后发现所有参赛学生的成绩均不低于50分.为了更好地了解本次大赛的成绩分布情况,随机抽取了部分参赛学生的成绩作为样本进行处理,得到下列不完整的统计图表.请你根据表中提供的信息,解答下列问题:| 分数段 | 频数 | 频率 |
| 50≤x<60 | 10 | 0.05 |
| 60≤x<70 | 30 | 0.15 |
| 70≤x<80 | 40 | n |
| 80≤x<90 | m | 0.35 |
| 90≤x≤100 | 50 | 0.25 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ${a^{-1}}=\frac{1}{a}$ | B. | (-a2)=-a2 | C. | $3{a^{-1}}=\frac{1}{3a}$ | D. | a0=1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{-9}$=-3 | B. | $\sqrt{144}$=±12 | C. | $\sqrt{{{({-7})}^2}}$=-7 | D. | ${({-\sqrt{2}})^2}$=2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,点P(x,y1)与Q(x,y2)分别是两个函数图象C1与C2上的任一点.当a≤x≤b时,有-1≤y1-y2≤1成立,则称这两个函数在a≤x≤b上是“相邻函数”,否则称它们在a≤x≤b上是“非相邻函数”.例如,点P(x,y1)与Q (x,y2)分别是两个函数y=3x+1与y=2x-1图象上的任一点,当-3≤x≤-1时,y1-y2=(3x+1)-(2x-1)=x+2,通过构造函数y=x+2并研究它在-3≤x≤-1上的性质,得到该函数值的范围是-1≤y≤1,所以-1≤y1-y2≤1成立,因此这两个函数在-3≤x≤-1上是“相邻函数”.
如图,点P(x,y1)与Q(x,y2)分别是两个函数图象C1与C2上的任一点.当a≤x≤b时,有-1≤y1-y2≤1成立,则称这两个函数在a≤x≤b上是“相邻函数”,否则称它们在a≤x≤b上是“非相邻函数”.例如,点P(x,y1)与Q (x,y2)分别是两个函数y=3x+1与y=2x-1图象上的任一点,当-3≤x≤-1时,y1-y2=(3x+1)-(2x-1)=x+2,通过构造函数y=x+2并研究它在-3≤x≤-1上的性质,得到该函数值的范围是-1≤y≤1,所以-1≤y1-y2≤1成立,因此这两个函数在-3≤x≤-1上是“相邻函数”.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com