
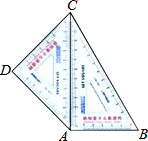
 如图,学生用三角板中,等腰直角三角形三角板的斜边靠在另一个含60°角的三角形板的对边上恰好完全重合,拼成一个四边形ABCD.若60°所对的直角边长为12cm,求拼成四边形ABCD的面积.
如图,学生用三角板中,等腰直角三角形三角板的斜边靠在另一个含60°角的三角形板的对边上恰好完全重合,拼成一个四边形ABCD.若60°所对的直角边长为12cm,求拼成四边形ABCD的面积. 分析 解Rt△ACD,得出AD=CD=$\frac{\sqrt{2}}{2}$AC=6$\sqrt{2}$,解Rt△ABC,得出AB=$\frac{\sqrt{3}}{3}$AC=4$\sqrt{3}$,然后分别求出这两个三角板的面积,再相加即可得到四边形ABCD的面积.
解答 解:∵在Rt△ACD中,∠D=90°,∠ACD=∠CAD=45°,
∴AD=CD=$\frac{\sqrt{2}}{2}$AC=6$\sqrt{2}$.
∵在Rt△ABC中,∠CAB=90°,∠B=60°,
∴AB=$\frac{\sqrt{3}}{3}$AC=4$\sqrt{3}$.
∵S△ACD=$\frac{1}{2}$AD•CD=$\frac{1}{2}$×6$\sqrt{2}$×6$\sqrt{2}$=36,
S△ABC=$\frac{1}{2}$AB•AC=$\frac{1}{2}$×4$\sqrt{3}$×12=24$\sqrt{3}$,
∴四边形ABCD的面积=S△ACD+S△ABC=36+24$\sqrt{3}$(cm2).
点评 本题考查了解直角三角形,锐角三角函数的定义,三角形的面积,求出AD、CD与AB是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
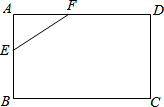 如图所示,将长方形ABCD切去一角后得到的五边形BCDEF的五条边长是17、19、23、27和38(顺序不一定按此排列),则五边形的面积是966.
如图所示,将长方形ABCD切去一角后得到的五边形BCDEF的五条边长是17、19、23、27和38(顺序不一定按此排列),则五边形的面积是966.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
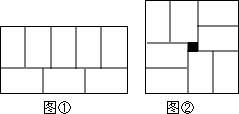 用8块相同的长方形地砖拼矩形,小明拼成了图①,小红拼成了图②,小红所拼图形中间刚好多出一个边长为1的小正方形,则每个小长方形的长宽分别为( )
用8块相同的长方形地砖拼矩形,小明拼成了图①,小红拼成了图②,小红所拼图形中间刚好多出一个边长为1的小正方形,则每个小长方形的长宽分别为( )| A. | 10,6 | B. | 15,9 | C. | 5,3 | D. | 20,12 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
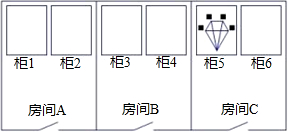 如图,有三间房,每间房内放有两个柜子,仅有一件宝物藏在某个柜子中,寻宝游戏规则如下:只允许进入三个房间中的一个房间并打开其中一个柜子即为一次游戏结束.找到宝物为游戏胜出,否则为游戏失败.
如图,有三间房,每间房内放有两个柜子,仅有一件宝物藏在某个柜子中,寻宝游戏规则如下:只允许进入三个房间中的一个房间并打开其中一个柜子即为一次游戏结束.找到宝物为游戏胜出,否则为游戏失败.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com