
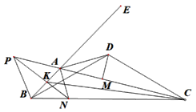
【题目】如图,DB=DC,∠BAC=∠BDC=120°,DM⊥AC,E为BA延长线上的点,∠BAC的角平分线交BC于N,∠ABC的外角平分线交CA的延长线于点P,连接PN交AB于K,连接CK,则下列结论正确的是:①∠ABD=∠ACD;②DA平分∠EAC;③当点A在DB左侧运动时,![]() 为定值;④∠CKN=30° ( )
为定值;④∠CKN=30° ( )
A.①③④B.②③④C.①②④D.①②③
【答案】C
【解析】
由∠BAC=∠BDC=120°可知ABCD四点共圆,由圆周角定理可得∠ABD=∠ACD,∠DAC=∠DBC=30°,即可得到∠DAC=∠EAD=30°,所以①②正确;无法得出③的结论,故③错误;PKN截△ABC,根据梅涅劳斯定理可得![]() ,再根据角平分线定理可推出
,再根据角平分线定理可推出![]() ,
,![]() ,从而得出
,从而得出![]() ,可知CK为∠ACB的角平分线,两条角平分线交点为△ABC的内心G,设△ANC的内心为H,易知H在CG上,连接AH,NH,可得角平分线,最后推出AKNH四点共圆,即可得∠CKN=∠NAH=30°,故④正确.
,可知CK为∠ACB的角平分线,两条角平分线交点为△ABC的内心G,设△ANC的内心为H,易知H在CG上,连接AH,NH,可得角平分线,最后推出AKNH四点共圆,即可得∠CKN=∠NAH=30°,故④正确.
解:∵∠BAC=∠BDC=120°
∴ABCD四点共圆,∠DBC=∠DCB=30°,如图所示,
∴∠ABD=∠ACD,∠DAC=∠DBC=30°,
故①正确;
又∵∠EAC=180°-∠BAC=60°,
∴∠EAD=∠EAC-∠DAC=30°=∠AEC
即AD平分∠EAC,故②正确;
无法得出③的结论,故③错误;
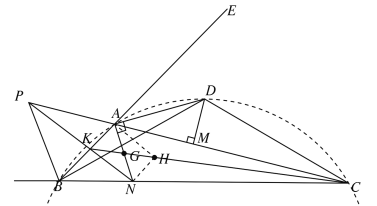
④PKN截△ABC,根据梅涅劳斯定理可得![]() ,
,
∵AN平分∠BAC,PB平分△ABC的外角,
∴![]() ,
,![]()
∴![]() ,整理得
,整理得![]()
∴CK平分∠ACB
AN,CK交于点G,则G为△ABC的内心,
设△ANC的内心为H,易知H在CG上,
连接AH,NH,则AH平分∠NAC,NH平分∠ANC
设∠ACB=![]() ,则∠ABC=
,则∠ABC=![]() ,
,
∴∠ANC=∠ABC+∠BAN=![]()
∴∠ANH=![]() ∠ANC=
∠ANC=![]()
又∵∠AKG=∠ABC+∠KCB=![]()
∴∠ANH=∠AKG
∴AKNH四点共圆,
∴∠CKN=∠NAH=30°,故④正确.
①②④正确,故选C.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】八(2)班组织了一次经典诵读比赛,甲、乙两队各10人的比赛成绩如下表(10分制):
甲 | 7 | 8 | 9 | 7 | 10 | 10 | 9 | 10 | 10 | 10 |
乙 | 10 | 8 | 7 | 9 | 8 | 10 | 10 | 9 | 10 | 9 |
(1)甲队成绩的中位数是 分,乙队成绩的众数是 分;
(2)计算乙队的平均成绩和方差;
(3)已知甲队成绩的方差是1.4,则成绩较为整齐的是 队.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线l:y=kx+1与抛物线y=x2-4x
(1)求证:直线l与该抛物线总有两个交点;
(2)设直线l与该抛物线两交点为A,B,O为原点,当k=-2时,求△OAB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC与△ADE中,∠BAC=∠DAE=90°,AD=AE,AB=AC,且B、D、E三点在一条直线上.
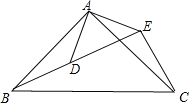
(1)求证:BD=CE.
(2)求∠BEC的度数.
(3)写出BE与AE、CE的数量关系是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地发生8.1级强烈地震,我国积极组织抢险队赴地震灾区参与抢险工作.如图,某探测队在地面A,B两处均探测出建筑物下方C处有生命迹象,已知探测线与地面的夹角分别是25°和60°,且AB=4米,求该生命迹象所在位置C的深度.(结果精确到1米.参考数据:sin25°≈0.4,cos25°≈0.9,tan25°≈0.5,![]() ≈1.7)
≈1.7)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,△ABC三个顶点的坐标分别是A(1,1),B (4,2),C(3,4).

(1)请画出△ABC关于y轴对称的△![]() ;
;
(2)△![]() 的面积为 ;
的面积为 ;
(3)在![]() 轴上求作一点P,使△PAB周长最小,请画出△PAB,并直接写出点P的坐标.
轴上求作一点P,使△PAB周长最小,请画出△PAB,并直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小明的父亲在相距![]() 米的两棵树间拴了一根绳子,给他做了一个简易的秋千,拴绳子的地方距地面高都是
米的两棵树间拴了一根绳子,给他做了一个简易的秋千,拴绳子的地方距地面高都是![]() 米,绳子自然下垂呈抛物线状,身高
米,绳子自然下垂呈抛物线状,身高![]() 米的小明距较近的那棵树
米的小明距较近的那棵树![]() 米时,头部刚好接触到绳子,则绳子的最低点距地面的距离为( )米.
米时,头部刚好接触到绳子,则绳子的最低点距地面的距离为( )米.

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=4,BC=5,点E是边CD的中点,将△ADE沿AE折叠后得到△AFE.延长AF交边BC于点G,则CG为_____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com