练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】正五边形广场 的边长为 米，甲、乙两个同学做游戏，分别从 、 两点处同时出发，沿 的方向绕广场行走，甲的速度为 ，乙的速度为 ，则两人第一次刚走到同一条边上时( )

    A. 甲在顶点 处 B. 甲在顶点 处 C. 甲在顶点处 D. 甲在顶点处

    【答案】D

    【解析】

    实际应用问题,见详解.

    解：两人如果在同一条边上,说明两人的距离小于等于80米,

    ∵甲、乙两个同学做游戏，分别从 、 两点处同时出发，两人相差160米,甲要追回80米需要的时间是80（50-46）=20分钟,

    20分钟甲走了1000米,正好走到CD的中点设为F;20分钟乙走920米走到DE距D点40米处设为G.

    甲从F走到D是40比50等于0.8分钟;乙用0.8分从G点走出0.8乘46等于36.8米距E点80-36.8-40=3.2米

    由此得知甲走到D点时乙走在DE线上距E3.2米处.

    ∴D选项是正确的

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】某中学团委会开展书法、诵读、演讲、征文四个项目（每人只参加一个项目）的比赛，初三（1）班全体同学都参加了比赛，为了解比赛的具体情况，小明收集整理数据后，绘制了以下不完整的折线统计图和扇形统计图，根据图表中的信息解答下列各题：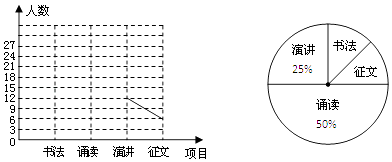
    （1）初三（1）班的总人数为 ， 扇形统计图中“征文”部分的圆心角度数为度；
    （2）请把折线统计图补充完整；
    （3）平平和安安两个同学参加了比赛，请用“列表法”或“画树状图法”，求出他们参加的比赛项目相同的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（感知）如图①，AB∥CD，点E在直线AB与CD之间，连结AE、BE，试说明∠BEE+∠DCE＝∠AEC．下面给出了这道题的解题过程，请完成下面的解题过程，并填空（理由或数学式）：

    解：如图①，过点E作EF∥AB

    ∴∠BAE＝∠1（　 　）

    ∵AB∥CD（　 　）

    ∴CD∥EF（　 　）

    ∴∠2＝∠DCE

    ∴∠BAE+∠DCE＝∠1+∠2（　 　）

    ∴∠BAE+∠DCE＝∠AEC

    （探究）当点E在如图②的位置时，其他条件不变，试说明∠AEC+∠FGC+∠DCE＝360°；

    （应用）点E、F、G在直线AB与CD之间，连结AE、EF、FG和CG，其他条件不变，如图③．若∠EFG＝36°，则∠BAE+∠AEF+∠FGC+∠DCG＝　 　°．

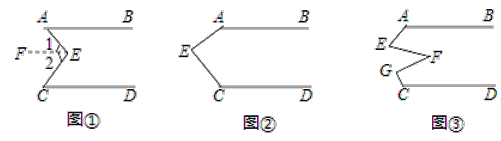
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，一艘轮船从点 A 向正北方向航行，每小时航行 15 海里，小岛P 在轮船的北偏西 15°，3 小时后轮船航行到点 B，小岛 P 此时在轮船的北偏西 30°方向，在小岛 P 的周围 20 海里范围内有暗礁，如果轮船不改变方向继续向前航行，是否会有触礁危险？请说明理由．

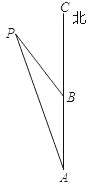
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在平面直角坐标系xOy中，若点P和点P1关于y轴对称，点P1和点P2关于直线l对称，则称点P2是点P关于y轴，直线l的二次对称点．
    （1）如图1，点A（﹣1，0）．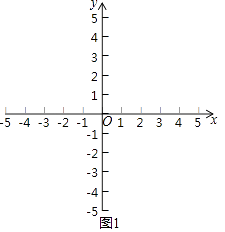
    ①若点B是点A关于y轴，直线l1：x=2的二次对称点，则点B的坐标为；
    ②若点C（﹣5，0）是点A关于y轴，直线l2：x=a的二次对称点，则a的值为；
    ③若点D（2，1）是点A关于y轴，直线l3的二次对称点，则直线l3的表达式为；
    （2）如图2，⊙O的半径为1．若⊙O上存在点M，使得点M'是点M关于y轴，直线l4：x=b的二次对称点，且点M'在射线y= x（x≥0）上，b的取值范围是；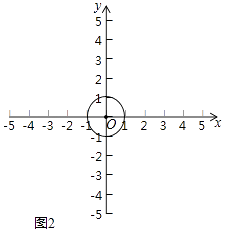
    （3）E（t，0）是x轴上的动点，⊙E的半径为2，若⊙E上存在点N，使得点N'是点N关于y轴，直线l5：y= x+1的二次对称点，且点N'在y轴上，求t的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

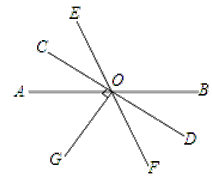
    【题目】如图，已知直线AB、CD、EF相交于点O，OG⊥CD，∠BOD＝36°．

    （1）求∠AOG的度数；

    （2）若OG是∠AOF的平分线，那么OC是∠AOE的平分线吗？说明你的理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】一次函数的图象经过点（-3，-2）．

    (1)求这个函数表达式；

    (2)判断（-5,3）是否在这个函数的图象上．

    (3)点M在直线y=kx+4上且到y轴的距离是3，求点M的坐标.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】中国古代有二十四节气歌，“春雨惊春清谷天，夏满芒夏暑相连．秋处露秋寒霜降，冬雪雪冬小大寒．”它是为便于记忆我国古时历法中二十四节气而编成的小诗歌，流传至今．节气指二十四时节和气候，是中国古代订立的一种用来指导农事的补充历法，是中国古代劳动人民长期经验的积累和智慧的结晶．其中第一个字“春”是指立春，为春季的开始，但在气象学上的入春日是有严格定义的，即连续5天的日平均气温稳定超过10℃又低于22℃，才算是进入春天，其中，5天中的第一天即为入春日．例如：2014年3月13日至18日，北京的日平均气温分别为9.3℃，11.7℃，12.7℃，11.7℃，12.7℃和12.3℃，即从3月14日开始，北京日平均气温已连续5天稳定超过10℃，达到了气象学意义上的入春标准．因此可以说2014年3月14日为北京的入春日． 日平均温度是指一天24小时的平均温度．气象学上通常用一天中的2时、8时、14时、20时4个时刻的气温的平均值作为这一天的日平均气温（即4个气温相加除以4），结果保留一位小数．
    如表是北京顺义2017年3月28日至4月3日的气温记录及日平均气温（单位：℃）

    时间

    2时

    8时

    14时

    20时

    平均气温

    3月28日

    6

    8

    13

    11

    9.5

    3月29日

    7

    6

    17

    14

    a

    3月30日

    7

    9

    15

    12

    10.8

    3月31日

    8

    10

    19

    13

    12.5

    4月1日

    8

    7

    18

    15

    12

    4月2日

    11

    7

    22

    16

    14

    4月3日

    13

    11

    21

    17

    15.5

    根据以上材料解答下列问题：
    （1）求出3月29日的日平均气温a；
    （2）采用适当的统计图将这7天的日平均气温的变化情况表示出来；
    （3）请指出2017年的哪一天是北京顺义在气象学意义上的入春日．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，直线AB交双曲线 于A，B两点，交x轴于点C，且BC= AB，过点B作BM⊥x轴于点M，连结OA，若OM=3MC，S△OAC=8，则k的值为多少？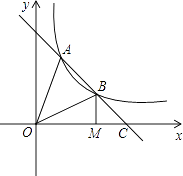

    查看答案和解析>>

    同步练习册答案