
【题目】如图,△OAB的一边OB在x轴的正半轴上,点A的坐标为(6,8),OA=OB,点P在线段OB上,点Q在y轴的正半轴上,OP=2OQ,过点Q作x轴的平行线分别交OA,AB于点E,F.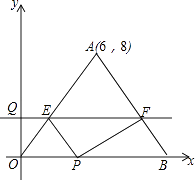
(1)求直线AB的解析式;
(2)若四边形POEF是平行四边形,求点P的坐标;
(3)是否存在点P,使△PEF为直角三角形?若存在,请直接写出点P的坐标;若不存在,请说明理由.
【答案】
(1)
解:∵A(6,8),∴OA= ![]() =10,
=10,
∴OB=OA=10,即B(10,0),
设直线AB解析式为y=kx+b,
把A与B坐标代入得: ![]() ,
,
解得:k=﹣2,b=20.
则直线AB解析式为y=﹣2x+20
(2)
解:由A(6,8),得到直线OA解析式为y= ![]() x,
x,
设OQ=t,则有OP=2OQ=2t,
把y=t代入y= ![]() x得:x=
x得:x= ![]() t;代入y=﹣2x+20得:x=10﹣
t;代入y=﹣2x+20得:x=10﹣ ![]() t,
t,
∴E( ![]() t,t),F(10﹣
t,t),F(10﹣ ![]() t,t),
t,t),
∴EF=10﹣ ![]() t﹣
t﹣ ![]() t=10﹣
t=10﹣ ![]() t,
t,
若四边形POEF为平行四边形,则有EF=OP,即10﹣ ![]() t=2t,
t=2t,
解得:t= ![]()
(3)
解:分三种情况考虑:
若∠PEF=90°,则有 ![]() t=2t,无解,不可能;
t=2t,无解,不可能;
若∠PFE=90°,则有10﹣ ![]() =2t,解得:t=4,此时OP=8,即P(8,0);
=2t,解得:t=4,此时OP=8,即P(8,0);
若∠EPF=90°,过E、F分别作x轴垂线,垂足分别为G、H,
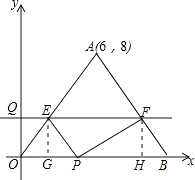
∴Rt△EGP∽Rt△PHF,
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
解得:t= ![]() ,此时P=
,此时P= ![]() ,即P(
,即P( ![]() ,0).
,0).
综上,P的坐标为(8,0)或( ![]() ,0)
,0)
【解析】(1)由A坐标确定出OA的长,即为OB的长,确定出B坐标,利用待定系数法求出直线AB解析式即可;(2)由A坐标确定出直线OA解析式,设OQ=t,则有OP=2t,表示出E与F坐标,进而表示出EF长,由四边形POEF为平行四边形,得到EF=OP,求出t的值,即可确定出P坐标;(3)分三种情况考虑:若∠PEF=90°;若∠PFE=90°;若∠EPF=90°,过E、F分别作x轴垂线,垂足分别为G、H,分别求出t的值,确定出满足题意P坐标即可.
【考点精析】认真审题,首先需要了解确定一次函数的表达式(确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法),还要掌握平行四边形的性质(平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分)的相关知识才是答题的关键.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=a,BC=b(a>b).在△ABC内依次作∠CBD=∠A,∠DCE=∠CBD,∠EDF=∠DCE.则EF等于( ) 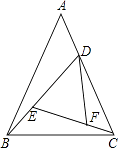
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为4cm,动点P、Q同时从点A出发,以1cm/s的速度分别沿A→B→C和A→D→C的路径向点C运动,设运动时间为x(单位:s),四边形PBDQ的面积为y(单位:cm2),则y与x(0≤x≤8)之间函数关系可以用图象表示为( )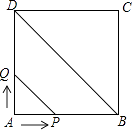
A.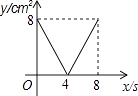
B.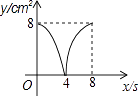
C.
D.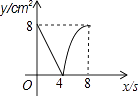
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=﹣x2+bx+c的图象经过坐标原点,与x轴交于点A(﹣2,0). 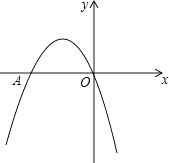
(1)求此二次函数的解析式;
(2)在抛物线上有一点P,满足S△AOP=1,请直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
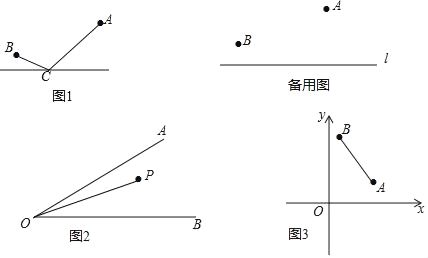
【题目】唐朝诗人李欣的诗《古从军行》开头两句说:“白日登山望峰火,黄昏饮马傍交河.”诗中隐含着一个有趣的数学问题我们称之为“饮马问题”.如图1所示,诗中将军在观望烽火之后从山脚下的A点出发,走到河旁边的C点饮马后再到B点宿营.请问怎样走才能使总的路程最短?某课题组在探究这一问题时抽象出数学模型:
直线l同旁有两个定点A、B,在直线l上存在点P,使得PA+PB的值最小.
解法:作点A关于直线l的对称点A′,连接A′B,则A′B与直线l的交点即为P,且PA+PB的最小值为线段A′B的长.
(1)根据上面的描述,在备用图中画出解决“饮马问题”的图形;
(2)利用轴对称作图解决“饮马问题”的依据是 .
(3)应用:①如图2,已知∠AOB=30°,其内部有一点P,OP=12,在∠AOB的两边分别有C、D两点(不同于点O),使△PCD的周长最小,请画出草图,并求出△PCD周长的最小值;
②如图3,点A(4,2),点B(1,6)在第一象限,在x轴、y轴上是否存在点D、点C,使得四边形ABCD的周长最小?若存在,请画出草图,并求其最小周长;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠CAB=65°,在同一平面内,将△ABC绕点A旋转到△AED的位置,使得DC∥AB,则∠BAE等于( ) 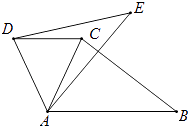
A.30°
B.40°
C.50°
D.60°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A的坐标为(2,0),点P在直线y=x上运动,当以点P为圆心,PA的长为半径的圆的面积最小时,点P的坐标为( )
A.(1,﹣1)
B.(0,0)
C.(1,1)
D.( ![]() ,
, ![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com