
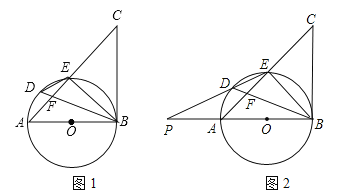
【题目】如图1,以△ABC的边AB为直径作⊙O,交AC边于点E,BD平分∠ABE交AC于F,交⊙O于点D,且∠BDE=∠CBE.
(1)求证:BC是⊙O的切线;
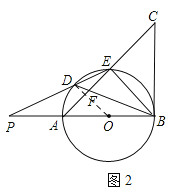
(2)延长ED交直线AB于点P,如图2,若PA=AO,DE=3,DF=2,求![]() 的值及AO的长.
的值及AO的长.
【答案】(1)答案见解析;(2)![]() ,AO=
,AO=![]() .
.
【解析】试题分析:(1)根据圆周角定理可知∠BAE+∠EBA=90°,由∠BAE=∠BDE,∠BDE=∠CBE,所以∠EBA+∠EBC=90°.
(2)易证OD∥DE,从而可知![]() ,易证△EDF∽△BDE,DE2=DFDB,从而可求出DB的长度,由勾股定理可知AB的长度.
,易证△EDF∽△BDE,DE2=DFDB,从而可求出DB的长度,由勾股定理可知AB的长度.
试题解析:解:(1)∵AB是直径,∴∠BAE+∠EBA=90°.∵∠BAE=∠BDE,∠BDE=∠CBE,∴∠EBA+∠EBC=90°,∴BC是⊙O的切线;
(2)连接OD.∵BD平分∠ABE,∴∠OBD=∠EBD.∵∠ODB=∠OBD,∴∠ODB=∠DBE,∴OD∥BE.∵PA=AO,∴![]() .∵∠DEF=∠DBA,∴∠DEF=∠EBD.∵∠EDF=∠EDB,∴△EDF∽△BDE,∴
.∵∠DEF=∠DBA,∴∠DEF=∠EBD.∵∠EDF=∠EDB,∴△EDF∽△BDE,∴![]() ,∴DE2=DFDB,∴DB=
,∴DE2=DFDB,∴DB=![]() ,∴由勾股定理可知:AB2=AD2+BD2,∴AB=
,∴由勾股定理可知:AB2=AD2+BD2,∴AB=![]() ,∴AO=
,∴AO=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,一次函数y=k1x﹣1的图象经过A(0,﹣1)、B(1,0)两点,与反比例函数y=![]() 的图象在第一象限内的交点为M,若△OBM的面积为1.
的图象在第一象限内的交点为M,若△OBM的面积为1.

(1)求一次函数和反比例函数的表达式;
(2)在x轴上是否存在点P,使AM⊥PM?若存在,求出点P的坐标;若不存在,说明理由;
(3)x轴上是否存在点Q,使△QBM∽△OAM?若存在,求出点Q的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
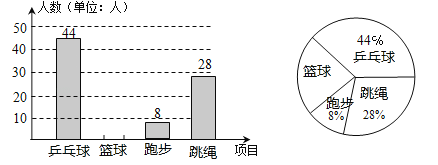
【题目】某校开展“阳光体育”活动,决定开设乒乓球、篮球、跑步、跳绳这四种运动项目,学生只能选择其中一种,为了解学生喜欢哪一种项目,随机抽取了部分学生进行调查,并将调查结果绘制成两张不完整的统计图,请你结合图中的信息解答下列问题:
(1)样本中喜欢篮球项目的人数百分比是 ;其所在扇形统计图中的圆心角的度数是 ;
(2)把条形统计图补画完整并注明人数;
(3)已知该校有1000名学生,根据样本估计全校喜欢乒乓球的人数是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,点E、F分别在边AB、BC上,且AE=![]() AB=2,将矩形沿直线EF折叠,点B恰好落在AD边上的点P处,连接BP交EF于点Q,下列结论:①EF=2BE;②△APE≌△QEB;③FQ=3EQ;④SBFPE=8
AB=2,将矩形沿直线EF折叠,点B恰好落在AD边上的点P处,连接BP交EF于点Q,下列结论:①EF=2BE;②△APE≌△QEB;③FQ=3EQ;④SBFPE=8![]() ,其中正确的结论是______(只填序号).
,其中正确的结论是______(只填序号).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程x2﹣(2k+3)x+k2+2k=0,有两个不相等的实数根x1,x2.
(1)求k的取值范围;
(2)若方程的两实数根x1,x2满足x1x2﹣x12﹣x22=﹣16,求实数k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在梯形ABCD中,AD∥BC,AB=CD,BC=10,对角线AC、BD相交于点O,且AC⊥BD,设AD=x,△AOB的面积为y.
(1)求∠DBC的度数;
(2)求y关于x的函数解析式,并写出自变量x的取值范围;
(3)如图1,设点P、Q分别是边BC、AB的中点,分别联结OP,OQ,PQ.如果△OPQ是等腰三角形,求AD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若关于x的三个方程x2+4mx+4m2+2m+3=0,x2+(2m+1)x+m2=0,(m﹣1)x2+2mx+m﹣1=0中至少有一个方程有实根,则m的取值范围是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,点E、F、G、H分别是边AB、BC、CD、DA的中点,顺次连接E、F、G、H,得到的四边形EFGH叫中点四边形.
(1)求证:四边形EFGH是平行四边形;
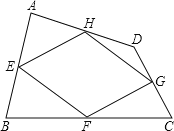
(2)如图,当四边形ABCD变成等腰梯形时,它的中点四边形是菱形,请你探究并填空:
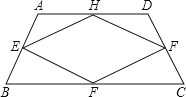
当四边形ABCD变成平行四边形时,它的中点四边形是 ;
当四边形ABCD变成矩形时,它的中点四边形是 ;
当四边形ABCD变成菱形时,它的中点四边形是 ;
当四边形ABCD变成正方形时,它的中点四边形是 ;
(3)根据以上观察探究,请你总结中点四边形的形状由原四边形的什么决定的?
查看答案和解析>>
科目:初中数学 来源: 题型:
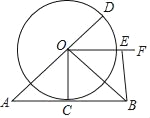
【题目】如图,在△ABO中,OA=OB,C是边AB的中点,以O为圆心的圆过点C,连接OC,AO延长线交⊙O于点D,OF是∠DOB的平分线,E为OF上一点,连接BE.
(1)求证:AB与⊙O相切;
(2)①当∠OEB=_____时,四边形OCBE为矩形;
②在①的条件下,若AB=4,则OA=_____时,四边形OCBE为正方形?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com