
【题目】如图,∠ABC=∠ACB,AD、BD、CD分别平分△ABC的外角∠EAC、内角∠ABC、外角∠ACF.以下结论:① AD∥BC;② ∠ACB=2∠ADB;③ ∠ADC=90°-∠ABD;④ BD平分∠ADC;⑤ 2∠BDC=∠BAC.其中正确的结论有 ( )
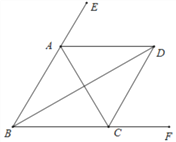
A. ①②④ B. ①③④⑤ C. ①②③⑤ D. ①②③④⑤
【答案】C
【解析】试题解析:(1)∵AD平分△ABC的外角∠EAC,
∴∠EAD=∠DAC,
∵∠EAC=∠ACB+∠ABC,且∠ABC=∠ACB,
∴∠EAD=∠ABC,
∴AD![]() BC,
BC,
故①正确.
(2)由(1)可知AD![]() BC,
BC,
∴∠ADB=∠DBC,
∵BD平分∠ABC,
∴∠ABD=∠DBC,
∴∠ABC=2∠ADB,
∵∠ABC=∠ACB,
∴∠ACB=2∠ADB,
故②正确.
(3)在△ADC中,∠ADC+∠CAD+∠ACD=180,
∵CD平分△ABC的外角∠ACF,
∴∠ACD=∠DCF,
∵AD![]() BC,
BC,
∴∠ADC=∠DCF,∠ADB=∠DBC,∠CAD=∠ACB
∴∠ACD=∠ADC,∠CAD=∠ACB=∠ABC=2∠ABD,
![]()
![]()
![]()
故③正确,
(4)如果BD平分∠ADC,则四边形ABCD是平行四边形,
∵∠ABD=∠ADB,
∴AB=AD,
∴四边形ABCD是菱形,
∴只有在△ABC是正三角形时才有BD平分∠ADC.
故④错误.
(5)∵∠BAC+∠ABC=∠ACF,
![]()
![]()
![]()
![]()
![]()
故⑤正确.
故选C.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图1,点O为直线AB上一点,过点O作射线OC,使∠AOC=60°,将一把直角三角尺的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方.
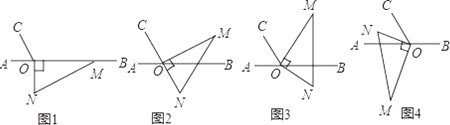
(1)将图1中的三角尺绕点O逆时针旋转至图2,使点N在OC的反向延长线上,请直接写出图中∠MOB的度数,∠MOB= .
(2)将图1中的三角尺绕点O逆时针旋转至图3,使一边OM在∠BOC的内部,且恰好平分∠BOC,求∠CON的度数.
(3)将图1中的三角尺绕点O顺时针旋转至图4,使ON在∠AOC的内部,请探究∠AOM与∠NOC之间的数量关系,并说明理由.
(4)将图1中的三角尺绕点O以每秒钟15°的转速顺时针旋转一周,当时间t为 秒钟时,ON所在的直线恰好平分∠AOC.(直接写答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将一条数轴在原点O和点B处各折一下,得到一条“折线数轴”.图中点A表示﹣11,点B表示10,点C表示18,我们称点A和点C在数轴上相距29个长度单位.动点P从点A出发,以2单位/秒的速度沿着“折线数轴”的正方向运动,从点O运动到点B期间速度变为原来的一半,之后立刻恢复原速;同时,动点Q从点C出发,以1单位/秒的速度沿着数轴的负方向运动,从点B运动到点O期间速度变为原来的两倍,之后也立刻恢复原速.设运动的时间为t秒.

问:(1)动点P从点A运动至C点需要多少时间?
(2)P、Q两点相遇时,求出相遇点M所对应的数是多少;
(3)求当t为何值时,P、O两点在数轴上相距的长度与Q、B两点在数轴上相距的长度相等.
查看答案和解析>>
科目:初中数学 来源: 题型:
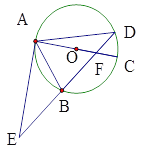
【题目】如图,已知⊙O的直径AC与弦BD相交于点F,点E是DB延长线上的一点,∠EAB=∠ADB;
(1)求证:AE是⊙O的切线;
(2)已知点B是EF的中点,求证:△EAF∽△CBA
(3)已知AF=4,CF=2,在(2)的条件下,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
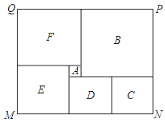
【题目】如图的长方形MNPQ是州某市民健身广场的平面示意图,它是由6个正方形拼成的(分别用A,B,C,D,E,F六个字母表示).已知中间最小的正方形A的边长是1米,设正方形C的边长是x米.
(1)请用含x的代数式分别表示出正方形EF和B的边长;
(2)观察图形的特点,找出两个等量关系,分别用两种方法列方程求出x的值;
(3)现沿着长方形广场的四条边铺设下水管道,若甲,乙两个工程队单独铺设分别需要10天和15天完成,如果两队从M处开始,分别沿两个不同方向同时施工![]() 天后,因甲队另有任务,余下的工程由乙队单独施工10天完成,求
天后,因甲队另有任务,余下的工程由乙队单独施工10天完成,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读下面某校八年级师生的对话内容,再解答问题.(温馨提示:一周只上五天课,另外考试时每半天考一科)
小明:“听说下周会进行连续两天的期中考试.”
刘老师:“是的,要考语文、数学、英语、物理共四科,但具体星期几不清楚.”
小宇:“我估计是星期四、星期五.”
(1)求小宇猜对的概率;
(2)若考试已定在星期四、星期五进行,但各科考试顺序没定,请用恰当的方法求同一天考语文、数学的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com