
如图,A、B是直线l上的两个点,C是l外的一点,△ABC的周长为32cm,A、B间的距离为10cm.
(1)补充图形画出△ABC关于直线l对称的△A′B′C′.
(2)一只蚂蚁从点A出发沿着A→C→B→C′的方向以每分钟10cm的速度返回A地,至少需要 分钟.
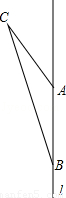
(1)如图
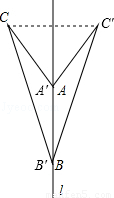
(2)4.4
【解析】
试题分析:(1)找出点C关于直线l的对称点C′的位置,A、A′,B、B′重合,然后顺次连接即可;
(2)先求出AC+BC的长度,再根据轴对称的性质求出蚂蚁行走的路程,然后根据时间=路程÷速度列式计算即可得解.
解:(1)△A′B′C′如图所示;
(2)∵△ABC的周长为32cm,A、B间的距离为10cm,
∴AC+BC=32﹣10=22cm,
∴蚂蚁行走的路程=22+22=44cm,
∵蚂蚁的速度是每分钟10cm,
∴时间=44÷10=4.4分钟.
故答案为:4.4.

点评:本题考查了利用轴对称变换作图,熟练掌握轴对称的性质,找出对应点的位置是解题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
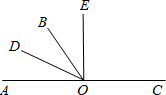 如图所示,O是直线AC上一点,OB是一条射线,OD平分∠AOB,OE在∠BOC内,∠BOE=
如图所示,O是直线AC上一点,OB是一条射线,OD平分∠AOB,OE在∠BOC内,∠BOE=| 1 | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
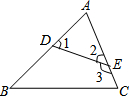 如图,∠
如图,∠查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com