
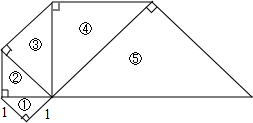
 一系列等腰直角三角形组成的螺旋形如图所示,其序号依次为①,②,③,④,⑤,…,则第n等腰直角三角形的斜边长为($\sqrt{2}$)n.
一系列等腰直角三角形组成的螺旋形如图所示,其序号依次为①,②,③,④,⑤,…,则第n等腰直角三角形的斜边长为($\sqrt{2}$)n. 分析 根据图形,先求出第一个等腰直角三角形的斜边,再在此基础上求出第二个等腰直角三角形是斜边,…以此类推,从而可求出第n个等腰直角三角形的斜边.
解答 解:如右图所示,
第一个等腰直角三角形的斜边=$\sqrt{{1}^{2}+{1}^{2}}$=$\sqrt{2}$,
第二个等腰直角三角形的斜边=$\sqrt{(\sqrt{2})^{2}+(\sqrt{2})^{2}}$=($\sqrt{2}$)2=2,
第三个等腰直角三角形的斜边=$\sqrt{{2}^{2}+{2}^{2}}$=($\sqrt{2}$)3,
…,
第n个等腰直角三角形的斜边=($\sqrt{2}$)n,
故答案是:($\sqrt{2}$)n.
点评 本题考查了等腰三角形的性质,勾股定理.关键是利用勾股定理求出每一个等腰直角三角形的斜边.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:初中数学 来源: 题型:解答题
 如图,抛物线y=-x2+bx+c经过点A(1,0),C(4,0),与y轴交于点B.
如图,抛物线y=-x2+bx+c经过点A(1,0),C(4,0),与y轴交于点B.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
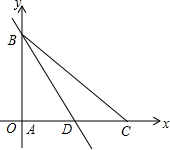 如图,△ABC中,∠BAC=90°,AB=AC=4,BD是AC边上的中线,分别以AC、AB所在直线为x轴、y轴建立直角坐标系.
如图,△ABC中,∠BAC=90°,AB=AC=4,BD是AC边上的中线,分别以AC、AB所在直线为x轴、y轴建立直角坐标系.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
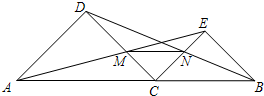 如图,已知C是线段AB上的任意一点(除端点外),分别以AC、BC为斜边并且在AB的同一侧作等腰直角△ACD和△BCE,连接AE交CD于点M,连接BD交CE于点N.
如图,已知C是线段AB上的任意一点(除端点外),分别以AC、BC为斜边并且在AB的同一侧作等腰直角△ACD和△BCE,连接AE交CD于点M,连接BD交CE于点N.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com