
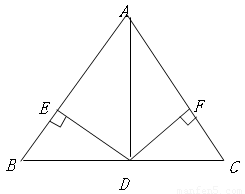
如图:已知在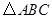 中,AD平分∠BAC,
中,AD平分∠BAC,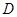 为
为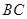 边的中点,过点
边的中点,过点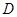 作
作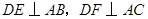 ,垂足分别为
,垂足分别为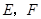 。
。
(1)求证: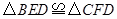 ;
;
(2)若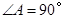 ,求证:四边形
,求证:四边形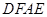 是正方形。
是正方形。
见解析
【解析】
试题分析:(1)由AD平分∠BAC,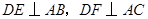 ,根据角平分线的性质即可得到DE=DF,再由
,根据角平分线的性质即可得到DE=DF,再由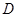 为
为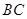 边的中点,即可证得结论;
边的中点,即可证得结论;
(2)由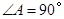 ,
,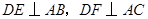 ,可得四边形
,可得四边形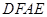 是矩形,再结合DE=DF即可证得结论。
是矩形,再结合DE=DF即可证得结论。
(1)∵AD平分∠BAC,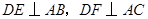 ,
,
∴DE=DF(角平分线上的点到角两边的距离相等),
∵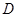 为
为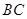 边的中点,
边的中点,
∴BD=CD,
∴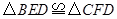 ;
;
(2)∵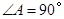 ,
,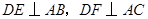 ,
,
∴四边形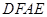 是矩形,
是矩形,
∵DE=DF,
∴矩形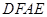 是正方形.
是正方形.
考点:本题考查的是全等三角形的判定和性质,正方形的判定
点评:判别一个四边形为正方形主要根据正方形的概念,途经有两种:①先说明它是矩形,再说明有一组邻边相等;②先说明它是菱形,再说明它有一个角为直角.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源: 题型:
 如图,已知△ABC中,AD平分∠BAC.
如图,已知△ABC中,AD平分∠BAC.| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
查看答案和解析>>
科目:初中数学 来源:2013届江苏扬州江都区双沟中学九年级10月练习数学试卷(带解析) 题型:解答题
如图:已知在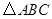 中,AD平分∠BAC,
中,AD平分∠BAC,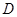 为
为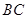 边的中点,过点
边的中点,过点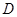 作
作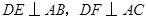 ,垂足分别为
,垂足分别为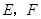 。
。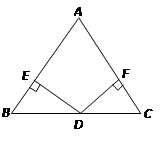
(1)求证: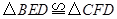 ;
;
(2)若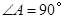 ,求证:四边形
,求证:四边形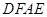 是正方形。
是正方形。
查看答案和解析>>
科目:初中数学 来源:2013届江苏省扬州市江都区麾村中学九年级第一次月考数学试卷(带解析) 题型:解答题
如图:已知在 中,AD平分∠BAC,
中,AD平分∠BAC, 为
为 边的中点,过点
边的中点,过点 作
作 ,垂足分别为
,垂足分别为 。
。
(1)求证: ;
;
(2)若 ,求证:四边形
,求证:四边形 是正方形。
是正方形。
查看答案和解析>>
科目:初中数学 来源:2012-2013学年江苏扬州江都区双沟中学九年级10月练习数学试卷(解析版) 题型:解答题
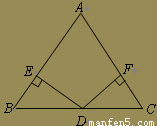
如图:已知在 中,AD平分∠BAC,
中,AD平分∠BAC,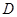 为
为 边的中点,过点
边的中点,过点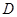 作
作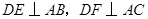 ,垂足分别为
,垂足分别为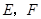 。
。
(1)求证: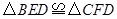 ;
;
(2)若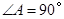 ,求证:四边形
,求证:四边形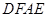 是正方形。
是正方形。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com