
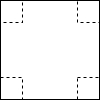
 如图,把一边长为xcm的正方形纸板的四个角各剪去一个边长为ycm的小正方形,然后把它折成一个无盖纸盒.
如图,把一边长为xcm的正方形纸板的四个角各剪去一个边长为ycm的小正方形,然后把它折成一个无盖纸盒.分析 (1)根据长方体的公式解答即可;
(2)根据纸盒的全面积=大正方形面积-4个小正方形面积,计算即可;
(3)如图由题意AD=2AE=2DF,推出EF=2AD=4AE,由此即可解决问题;
解答 解:(1)y(x-2y)2化简后为:x2y-4xy2+4y3
所以该纸盒的体积为(x2y-4xy2+4y3)cm3
(2)x2-4y2
所以该纸盒的全面积为(x2-4y2)cm2
(3)结论:x=4y.
理由:如图由题意AD=2AE=2DF,
∴EF=2AD=4AE,
∵EF=x,AE=y,
∴x=4y.
点评 此题主要考查了列代数式及求代数式的值、长方体的体积公式、表面积等知识,解题的关键是正确题意,然后根据题目的数量关系列出代数式解决问题.


科目:初中数学 来源: 题型:解答题
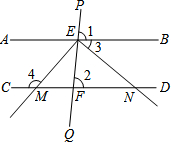 已知:如图,直线PQ分别与直线AB、CD交于点E和点F,∠1=∠2,射线EM、EN分别与直线CD交于点M、N,且EM⊥EN,∠3=40°,求∠4的度数.
已知:如图,直线PQ分别与直线AB、CD交于点E和点F,∠1=∠2,射线EM、EN分别与直线CD交于点M、N,且EM⊥EN,∠3=40°,求∠4的度数.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 24cm2 | B. | 36cm2 | C. | 48cm2 | D. | 60cm2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
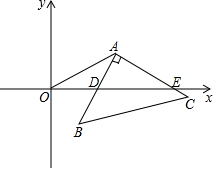 如图,平面直角坐标系中有一点A(a,b),且满足$\sqrt{a-8}$+(b-4)2=0,将Rt△ABC的直角顶点与A重合并绕直角顶点A旋转,直角边AB与x轴始终交于D,连接OA.
如图,平面直角坐标系中有一点A(a,b),且满足$\sqrt{a-8}$+(b-4)2=0,将Rt△ABC的直角顶点与A重合并绕直角顶点A旋转,直角边AB与x轴始终交于D,连接OA.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com