
分析 (1)求出方程的判别式△的值,利用配方法得出△>0,根据判别式的意义即可证明;
(2)由于二次函数y=x2+(k-5)x+1-k的图象不经过第三象限,又△=(k-5)2-4(1-k)=(k-3)2+12>0,所以抛物线的顶点在x轴的下方经过一、二、四象限,根据二次项系数知道抛物线开口向上,由此可以得出关于k的不等式组,解不等式组即可求解;
(3)设方程的两个根分别是x1,x2,根据题意得(x1-3)(x2-3)<0,根据一元二次方程根与系数的关系求得k的取值范围,再进一步求出k的最大整数值.
解答 (1)证明:∵△=(k-5)2-4(1-k)=k2-6k+21=(k-3)2+12>0,
∴无论k为何值,方程总有两个不相等实数根;
(2)解:∵二次函数y=x2+(k-5)x+1-k的图象不经过第三象限,
∵二次项系数a=1,
∴抛物线开口方向向上,
∵△=(k-3)2+12>0,
∴抛物线与x轴有两个交点,
设抛物线与x轴的交点的横坐标分别为x1,x2,
∴x1+x2=5-k>0,x1•x2=1-k≥0,
解得k≤1,
即k的取值范围是k≤1;
(3)解:设方程的两个根分别是x1,x2,
根据题意,得(x1-3)(x2-3)<0,
即x1•x2-3(x1+x2)+9<0,
又x1+x2=5-k,x1•x2=1-k,
代入得,1-k-3(5-k)+9<0,
解得k<$\frac{5}{2}$.
则k的最大整数值为2.
点评 本题考查了抛物线与x轴的交点,二次函数的图象和性质,二次函数与一元二次方程的关系,根的判别式,根与系数的关系,综合性较强,难度适中.


 优等生题库系列答案
优等生题库系列答案 53天天练系列答案
53天天练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
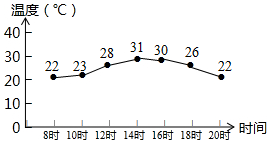 如图是根据我市某天七个整点时的气温绘制成的统计图,则这七个整点时气温的中位数和平均数分别是( )
如图是根据我市某天七个整点时的气温绘制成的统计图,则这七个整点时气温的中位数和平均数分别是( )| A. | 30,28 | B. | 26,26 | C. | 31,30 | D. | 26,22 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
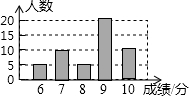 如图是根据“红星中学”903班所有学生的立定跳远成绩制作的条形统计图,下列说法中不正确的是( )
如图是根据“红星中学”903班所有学生的立定跳远成绩制作的条形统计图,下列说法中不正确的是( )| A. | 该校903班有50名学生 | B. | 这组数据的众数是7分和8分 | ||
| C. | 这组数据的中位数是9分 | D. | 这组数据的平均数是8.4分 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 40% | B. | B56% | C. | 60% | D. | 62% |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x<$\frac{1}{2}$ | B. | x≤$\frac{1}{2}$ | C. | x>$\frac{1}{2}$ | D. | x≥$\frac{1}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com