
 ,0),点B在x轴上方且BA⊥x轴,
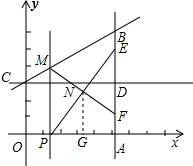
,0),点B在x轴上方且BA⊥x轴, ,过点C作CD⊥AB于D,点P是线段OA上一动点,PM∥AB交BC于点M,交CD于点Q,以PM为斜边向右作直角三角形PMN,∠MPN=30°,PN、MN的延长线交直线AB于E、F,设PO的长为x,EF的长为y.
,过点C作CD⊥AB于D,点P是线段OA上一动点,PM∥AB交BC于点M,交CD于点Q,以PM为斜边向右作直角三角形PMN,∠MPN=30°,PN、MN的延长线交直线AB于E、F,设PO的长为x,EF的长为y.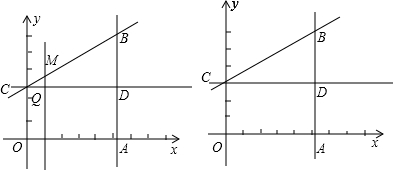

 ,0),
,0), ,
, ,
,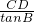 =3,
=3,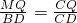 ,
,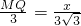 ,
, x,
x, x;
x;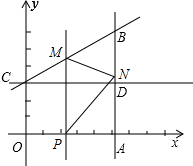 (2)∵∠PNM=90°,∠MPN=30°,
(2)∵∠PNM=90°,∠MPN=30°,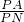 =
= ,
, -x),
-x), PM=
PM= (3+
(3+ x),
x), -x)=
-x)= (3+
(3+ x),
x),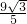 ;
; ,m),
,m),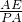 =
=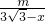 =
= ,
, x,
x, ,9-
,9- x),
x),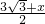 ,
,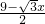 ),
),
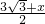 -x=
-x=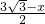 ,
, -x,
-x,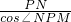 =
=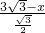 =6-
=6- x,
x, x=3+
x=3+ x,
x, ,
, ,0),点E的坐标为(3
,0),点E的坐标为(3 ,6),
,6),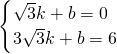 ,
,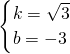 ,
, x-3;
x-3; PM,
PM, PN=
PN= PM,PG=PN•cos∠NPG=
PM,PG=PN•cos∠NPG= PN=
PN= PM,
PM, PM+x,点N的纵坐标为
PM+x,点N的纵坐标为 PM,
PM,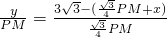 ,
, x=12-(3+
x=12-(3+ x)-
x)- x=9-
x=9- x,
x,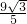 ).
).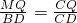 ,则可求得MQ的值,继而求得PM的值;
,则可求得MQ的值,继而求得PM的值; -x)=
-x)= (3+
(3+ x),解此方程即可求得答案;
x),解此方程即可求得答案; ,m),利用三角函数的知识即可求得点E的坐标为:(3
,m),利用三角函数的知识即可求得点E的坐标为:(3 ,9-
,9- x),又由PE是线段MF的垂直平分线,可求得点N的坐标,继而可得方程6-
x),又由PE是线段MF的垂直平分线,可求得点N的坐标,继而可得方程6- x=3+
x=3+ x,解此方程则可求得点P与E的坐标,再利用待定系数法即可求得此直线的解析式;
x,解此方程则可求得点P与E的坐标,再利用待定系数法即可求得此直线的解析式;

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
 (2012•桂平市三模)如图,点P的坐标为(2,
(2012•桂平市三模)如图,点P的坐标为(2,| 3 |
| 2 |
| k |
| x |
| k |
| x |
查看答案和解析>>
科目:初中数学 来源: 题型:
 已知:在直角坐标系中,点C的坐标为(0,-2),点A与点B在x轴上,且点A与点B的横坐标是方程x2-3x-4=0的两个根,点A在点B的左侧.
已知:在直角坐标系中,点C的坐标为(0,-2),点A与点B在x轴上,且点A与点B的横坐标是方程x2-3x-4=0的两个根,点A在点B的左侧.查看答案和解析>>
科目:初中数学 来源: 题型:
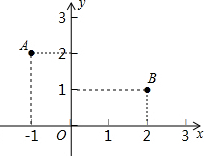 如图,点A的坐标为(-1,2),点B的坐标为(2,1),有一点C在x轴上移动,则点C到A、B两点的距离之和的最小值为( )
如图,点A的坐标为(-1,2),点B的坐标为(2,1),有一点C在x轴上移动,则点C到A、B两点的距离之和的最小值为( )A、3
| ||
| B、4 | ||
| C、3 | ||
D、4
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com