
分析 先利用立方和公式分解得到原式=[$\frac{2}{\sqrt{a}-\sqrt{b}}$-$\frac{2\sqrt{a}}{(\sqrt{a}+\sqrt{b})(a-\sqrt{ab}+b)}$•$\frac{a-\sqrt{ab}+b}{\sqrt{a}-\sqrt{b}}$]÷4$\sqrt{ab}$,再约分后把括号内通分,然后进行二次根式的除法运算.
解答 解:原式=[$\frac{2}{\sqrt{a}-\sqrt{b}}$-$\frac{2\sqrt{a}}{(\sqrt{a}+\sqrt{b})(a-\sqrt{ab}+b)}$•$\frac{a-\sqrt{ab}+b}{\sqrt{a}-\sqrt{b}}$]÷4$\sqrt{ab}$
=[$\frac{2(\sqrt{a}+\sqrt{b})}{(\sqrt{a}+\sqrt{b})(\sqrt{a}-\sqrt{b})}$-$\frac{2\sqrt{a}}{(\sqrt{a}+\sqrt{b})(\sqrt{a}-\sqrt{b})}$]÷4$\sqrt{ab}$
=$\frac{2\sqrt{b}}{a-b}$÷4$\sqrt{ab}$
=$\frac{\sqrt{a}}{2{a}^{2}-2ab}$.
点评 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.


科目:初中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{2}}{3}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{\sqrt{5}}{3}$ | D. | $\frac{\sqrt{6}}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
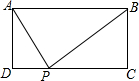 如图,矩形ABCD中,AB>AD,P为CD上异于C、D的一动点,且△APB为直角三角形,
如图,矩形ABCD中,AB>AD,P为CD上异于C、D的一动点,且△APB为直角三角形,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,∠CAB的平分线AD与BC垂直平分线DE交于点D,DM⊥AB于点M,DN⊥AC,交AC的延长线于点N,求证:BM=CN.
如图,在△ABC中,∠CAB的平分线AD与BC垂直平分线DE交于点D,DM⊥AB于点M,DN⊥AC,交AC的延长线于点N,求证:BM=CN.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
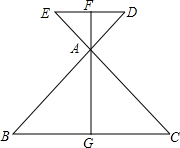 如图所示,BD与CE相交于点A,且AB=AC,AD=AE,△ABC的中线AG的反向延长线交DE于点F,则AF与DE垂直吗?用“三线合一”的方法说明理由.
如图所示,BD与CE相交于点A,且AB=AC,AD=AE,△ABC的中线AG的反向延长线交DE于点F,则AF与DE垂直吗?用“三线合一”的方法说明理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com