练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    10．若3a=2b=4c，且abc≠0，则$\frac{a+b}{c-2a}$的值是（　　）
    A．2B．3C．-2D．-3

    分析 根据已知求出a=$\frac{4}{3}$c，b=2c，代入求出即可．

    解答 解：∵3a=2b=4c，
    ∴a=$\frac{4}{3}$c，b=2c，
    ∴$\frac{a+b}{c-2a}$=$\frac{\frac{4}{3}c+2c}{c-2×\frac{4}{3}c}$=-2．
    故选C．

    点评 本题考查了比例的性质，分式的混合运算的应用，能求出a=$\frac{4}{3}$c和b=2c是解此题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    20．已知，如图，AB∥CD，∠DCF=100°，则∠AEF的度数为（　　）
    A．120°B．110°C．100°D．80°

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    1．求当x-9不小于-x+7时，x的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

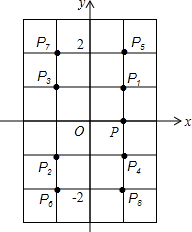    18．如图所示，在平面直角坐标系中，点P（1，0）作如下实验：先向上平移（后一次平移比上一次多1个单位长度），再作关于原点的对称点，即向上平移1个单位得到点P1，作点P1关于原点的对称点P2，再向上平移2个单位得到P3，作P3关于原点的对称点P4…，那么点P2015的坐标是（-1，504）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    5．如图，直线l1∥l2∥l3，另两条直线分别交l1，l2，l3于点A，B，C及点D，E，F，且AB=3，DE=4，EF=2，则：
    ①BC：AB=$\frac{1}{2}$；
    ②AB：AC=$\frac{2}{3}$；
    ③BC•DE=6；
    ④BC•EF=12．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    15．若a、b、c都不等于0，且$\frac{|a|}{a}$+$\frac{|b|}{b}$+$\frac{|c|}{c}$的最大值是m，最小值是n，求2013（m+n）+m-n的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

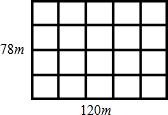    2．一块矩形耕地大小尺寸如图所示，要在这块地上沿东西南北方向分别挖4条和3条水渠，如果水渠的宽相等，而且要保证余下的可耕地而积为8700m2，那么水渠要挖多宽？

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    19．如图，△ABC的面积为2cm2，AP与∠B的平分线垂直，垂足是点P，则△PBC的面积为1cm2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    20．求下面各式中x的值：
    （1）px•p6=p2x（p≠0且p≠1）；
    （2）8×2x=2×22x．

    查看答案和解析>>

    同步练习册答案