
【题目】如图,长方形![]() 中,
中,![]() ,
,![]() ,长方形内有一个点
,长方形内有一个点![]() ,连结
,连结![]() ,
,![]() ,
,![]() ,已知
,已知![]() ,
,![]() ,延长
,延长![]() 交
交![]() 于点
于点![]() ,则
,则![]() _____________.
_____________.
【答案】![]()
【解析】
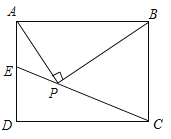
延长AP交CD于F,根据已知条件得到∠CPF+∠CPB=90°,根据矩形的性质得到∠DAB=∠ABC=90°,BC=AD=3,根据余角的性质得到∠EAP=∠ABP,推出AE=PE,根据勾股定理即可得到结论.
延长AP交CD于F,
∵∠APB=90°,
∴∠FPB=90°,
∴∠CPF+∠CPB=90°,
∵四边形ABCD是矩形,
∴∠DAB=∠ABC=90°,BC=AD=3,
∴∠EAP+∠BAP=∠ABP+∠BAP=90°,
∴∠EAP=∠ABP,
∵CP=CB=3,
∴∠CPB=∠CBP,
∴∠CPF=∠ABP=∠EAP,
∵∠EPA=∠CPF,
∴∠EAP=∠APE,
∴AE=PE,
∵CD2+DE2=CE2,
∴42+(3-AE)2=(3+AE)2,
解得AE=![]() .
.
故![]() .
.
故答案为:![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
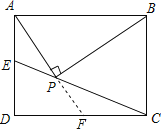
【题目】如下图,正方形ABCD的边AB在x轴上,A(﹣4,0),B(﹣2,0),定义:若某个抛物线上存在一点P,使得点P到正方形ABCD四个顶点的距离相等,则称这个抛物线为正方形ABCD的“友好抛物线”.若抛物线y=2x2﹣nx﹣n2﹣1是正方形ABCD的“友好抛物线”,则n的值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
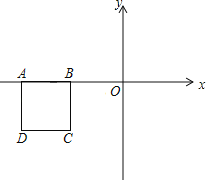
【题目】如图,在正方形ABCD中,AB=4cm,动点E从点A出发,以1cm/秒的速度沿折线AB—BC的路径运动,到点C停止运动.过点E作 EF∥BD,EF与边AD(或边CD)交于点F,EF的长度y(cm)与点E的运动时间x(秒)的函数图象大致是

A.  B.
B. 
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
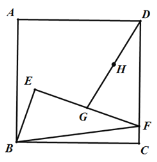
【题目】如图,E为正方形ABCD内一点,点F在CD边上,且∠BEF=90°,EF=2BE.点G为EF的中点,点H为DG的中点,连接EH并延长到点P,使得PH=EH,连接DP.
(1)依题意补全图形;
(2)求证:DP=BE;
(3)连接EC,CP,猜想线段EC和CP的数量关系并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC内接于⊙O,AC是⊙O的直径,D是![]() 的中点.过点D作CB的垂线,分别交CB、CA延长线于点F、E.
的中点.过点D作CB的垂线,分别交CB、CA延长线于点F、E. 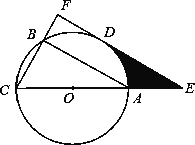
(1)判断直线EF与⊙O的位置关系,并说明理由;
(2)若CF=6,∠ACB=60°,求阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BD=BE,∠D=∠E,∠ABC=∠DBE=90°,BF⊥AE,且点A,C,E在同一条直线上.
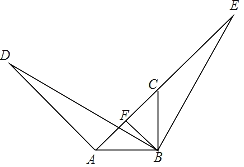
(1)求证:△DAB≌△ECB;
(2)若AD=3,AF=1,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,点D在边BC上,点E在边AC上,且AD=AE.
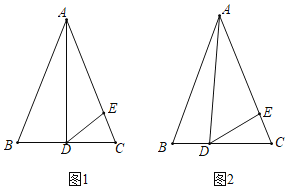
(1)如图1,当AD是边BC上的高,且∠BAD=30°时,求∠EDC的度数;
(2)如图2,当AD不是边BC上的高时,请判断∠BAD与∠EDC之间的关系,并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
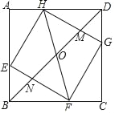
【题目】在边长为3的正方形ABCD中,点E、F、G、H分别在AB、BC、CD、DA边上,且满足EB=FC=GD=HA=1,BD分别与HG、HF、EF相交于M、O、N给出以下结论:
①HO=OF;②OF2=ONOB;③HM=2MG;④S△HOM=![]() ,其中正确的个数有( )
,其中正确的个数有( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
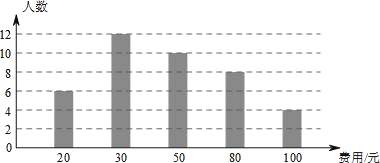
【题目】在全民读书月活动中,某校随机抽样调查了一部分学生本学期计划购买课外书的费用情况,根据图中的相关信息,解答下面问题;
(1)这次调查获取的样本容量是 ;
(2)由统计图可知,这次调查获取的样本数据的众数是 ;中位数是 ;
(3)求这次调查获取的样本数据的平均数;
(4)若该校共有1000名学生,根据样本数据,估计该校本学期计划购买课外书的总花费.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com