
【题目】已知如图1:△ABC中,AB=AC,∠B、∠C的平分线相交于点O,过点O作EF∥BC交AB、AC于E、F.
(1)图中有几个等腰三角形?请说明EF与BE、CF间有怎样的关系. 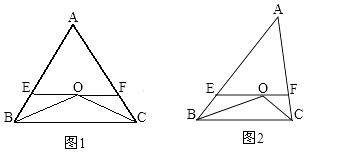
(2)若AB≠AC,其他条件不变,如图2,图中还有等腰三角形吗?如果有,请分别指出它们.另第(1)问中EF与BE、CF间的关系还存在吗?
(3)若△ABC中,∠B的平分线与三角形外角∠ACD的平分线CO交于O,过O点作OE∥BC交AB于E,交AC于F.如图3,这时图中还有哪几个等腰三角形?EF与BE、CF间的关系如何?为什么? 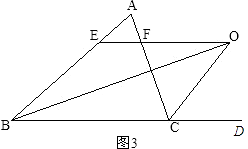
【答案】
(1)解:有5个等腰三角形,EF与BE、CF间有怎样的关系是:EF=BE+CF=2BE=2CF.理由如下:
∵EF∥BC,
∴∠EOB=∠OBC,∠FOC=∠OCB,
又∠B、∠C的平分线交于O点,
∴∠EBO=∠OBC,∠FCO=∠OCB,
∴∠EOB=∠OBE,∠FCO=∠FOC,
∴OE=BE,OF=CF,
∴EF=OE+OF=BE+CF.
又AB=AC,
∴∠ABC=∠ACB,
∴∠EOB=∠OBE=∠FCO=∠FOC,
∴EF=BE+CF=2BE=2CF;
(2)有2个等腰三角形分别是:等腰△OBE和等腰△OCF;
第一问中的EF与BE,CF的关系是:EF=BE+CF.
(3)有,还是有2个等腰三角形,△EBO,△OCF,EF=BE﹣CF,理由如下:
∵EO∥BC,
∴∠EOB=∠OBC,∠EOC=∠OCG(G是BC延长线上的一点)
又∵OB,OC分别是∠ABC与∠ACG的角平分线
∴∠EBO=∠OBC,∠ACO=∠OCD,
∴∠EOB=∠EBO,
∴BE=OE,
∠FCO=∠FOC,
∴CF=FO,
又∵EO=EF+FO,
∴EF=BE﹣CF.
【解析】(1)根据EF∥BC,∠B、∠C的平分线交于O点,可得∠EOB=∠OBC,∠FOC=∠OCB,∠EOB=∠OBE,∠FCO=∠FOC,再加上题目中给出的AB=AC,共5个等腰三角形;根据等腰三角形的性质,即可得出EF与BE、CF间有怎样的关系.(2)根据EF∥BC 和∠B、∠C的平分线交于O点,还可以证明出△OBE和△OCF是等腰三角形;利用几个等腰三角形的性质即可得出EF与BE,CF的关系.(3)EO∥BC和OB,OC分别是∠ABC与∠ACL的角平分线,还可以证明出△BEO和△CFO是等腰三角形.
【考点精析】掌握平行线的性质是解答本题的根本,需要知道两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补.


科目:初中数学 来源: 题型:
【题目】如图所示,在△ABC中,∠C=90°,AD是∠BAC的平分线,DE⊥AB交AB于E,F在AC上,∠B=∠CFD. 证明: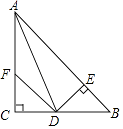
(1)CF=EB
(2)AB=AF+2EB.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:关于三角函数还有如下的公式:
sin(α±β)=sinαcosβ±cosαsinβ
tan(α±β)=![]()
利用这些公式可以将一些不是特殊角的三角函数转化为特殊角的三角函数来求值.
例:tan75°=tan(45°+30°)=![]() =
=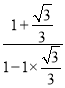 =
=![]()
根据以上阅读材料,请选择适当的公式解答下面问题:
(1)计算:sin15°;
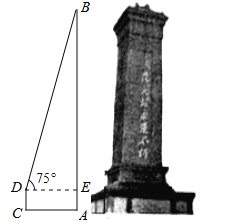
(2)某校在开展爱国主义教育活动中,来到烈士纪念碑前缅怀和纪念为国捐躯的红军战士.李三同学想用所学知识来测量如图纪念碑的高度.已知李三站在离纪念碑底7米的C处,在D点测得纪念碑碑顶的仰角为75°,DC为![]() 米,请你帮助李三求出纪念碑的高度.
米,请你帮助李三求出纪念碑的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某天,小华在一条东西方向的公路上行走,他从家里出发,如果把向东350米记作-350米,那么他折回来行走280米表示什么意思?这时,他停下来休息,休息的地方在他家的什么方向上?距家有多远?小华共走了多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列运算正确的是( )
A. ﹣2x2﹣3x2=﹣5x2 B. 6x2y3+2xy2=3xy
C. 2x33x2=6x6 D. (a+b)2=a2﹣2ab+b2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题正确的是( )
A.顺次连结矩形各边的中点所得的四边形是菱形
B.任意多边形的内角和为360°
C.一组对边平行,另一组对边相等的四边形是平行四边形
D.对角线相等的四边形是矩形
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com