
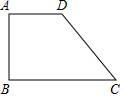
 如图,梯形ABCD中,∠ABC=∠BAD=90°,AD=AB=1,∠BCD=45°.将梯形ABCD折叠,使得点C与点A重合,折痕交CD于E,交BC于F,画出图形.求出折叠后重叠部分的面积.
如图,梯形ABCD中,∠ABC=∠BAD=90°,AD=AB=1,∠BCD=45°.将梯形ABCD折叠,使得点C与点A重合,折痕交CD于E,交BC于F,画出图形.求出折叠后重叠部分的面积. 分析 先过D作DG⊥BC于G,根据四边形ABGD是正方形,△CDG是等腰直角三角形,得到BC=2,再根据勾股定理即可得到CF的长,再延长折痕FE交AD的延长线于Q,根据△AOQ≌△COF,即可得出AQ=CF=$\frac{5}{4}$,最后过E作EH⊥CF于H,交AQ于P,根据△DEQ∽△CEF,即可得出HE=$\frac{5}{6}$PH=$\frac{5}{6}$,据此可得△CEF的面积为$\frac{25}{48}$,进而得出折叠后△AEF的面积为$\frac{25}{48}$.
解答 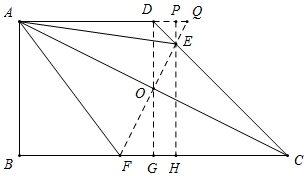 解:如图所示,连接AC,作AC的垂直平分线EF,连接AE,AF,则EF即为折痕,△AEF即为折叠后重叠部分,过D作DG⊥BC于G,则四边形ABGD是正方形,△CDG是等腰直角三角形,
解:如图所示,连接AC,作AC的垂直平分线EF,连接AE,AF,则EF即为折痕,△AEF即为折叠后重叠部分,过D作DG⊥BC于G,则四边形ABGD是正方形,△CDG是等腰直角三角形,
∴BC=BG+CG=2,
设CF=x=AF,则BF=2-x,
∴Rt△ABF中,12+(2-x)2=x2,
解得x=$\frac{5}{4}$,
∴CF=$\frac{5}{4}$,
延长FE交AD的延长线于Q,
∵∠AOQ=∠COF,∠Q=∠CFO,AO=CO,
∴△AOQ≌△COF,
∴AQ=CF=$\frac{5}{4}$,
又∵AD=1,
∴DQ=$\frac{1}{4}$,
过E作EH⊥CF于H,交AQ于P,
∵DQ∥CF,
∴△DEQ∽△CEF,
∴$\frac{PE}{HE}$=$\frac{DQ}{CF}$=$\frac{1}{5}$,
又∵PH=DG=1,
∴HE=$\frac{5}{6}$PH=$\frac{5}{6}$,
∴△CEF的面积=$\frac{1}{2}$CF×EH=$\frac{1}{2}$×$\frac{5}{4}$×$\frac{5}{6}$=$\frac{25}{48}$,
由折叠可得,△AEF的面积=△CEF的面积=$\frac{25}{48}$,
∴折叠后重叠部分的面积为$\frac{25}{48}$.
点评 本题主要考查了折叠问题,梯形的性质以及轴对称的性质的运用,解决问题的关键作辅助线构造全等三角形以及相似三角形,依据全等三角形对应边相等以及相似三角形的对应边成比例,求得△CEF的面积.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
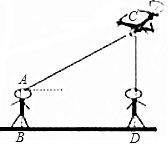 我区中小学生广播操比赛中,无人机对此次比赛的全过程进行了航拍,如图,某一时刻,无人机刚好飞至小琪头顶上方,而站在离小琪35米远的小珺仰望无人机,仰角为36°,已知小珺的眼睛离地面的距离AB为1.63m,那么此时无人机离地面大约有多高?(结果精确到0.1m)(参考数据:sin36°≈0.59,cos36°≈0.81,tan36°≈0.73)
我区中小学生广播操比赛中,无人机对此次比赛的全过程进行了航拍,如图,某一时刻,无人机刚好飞至小琪头顶上方,而站在离小琪35米远的小珺仰望无人机,仰角为36°,已知小珺的眼睛离地面的距离AB为1.63m,那么此时无人机离地面大约有多高?(结果精确到0.1m)(参考数据:sin36°≈0.59,cos36°≈0.81,tan36°≈0.73)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
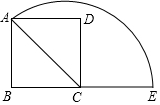 如图,在正方形ABCD中,AB=2,连接AC,以点C为圆心、AC长为半径画弧,与BC的延长线交于点E,则图中$\widehat{AE}$的长为$\frac{3\sqrt{2}}{2}$π.
如图,在正方形ABCD中,AB=2,连接AC,以点C为圆心、AC长为半径画弧,与BC的延长线交于点E,则图中$\widehat{AE}$的长为$\frac{3\sqrt{2}}{2}$π.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com