【题目】如图，在平面直角坐标系中，△ABC的三个顶点分别为A（﹣1，﹣1），B（﹣3，3），C（﹣4，1）
（1）画出△ABC关于y轴对称的△A1B1C1 ， 并写出点B的对应点B1的坐标；
（2）画出△ABC绕点A按逆时针旋转90°后的△AB2C2 ， 并写出点C的对应点C2的坐标．
【答案】
（1）
解：如图所示，△A1B1C1即为△ABC关于y轴对称的图形；
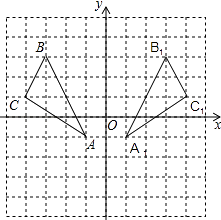
则B1的坐标是（3，3）
（2）
解：△ABC绕点A按逆时针旋转90°后的△AB2C2是：
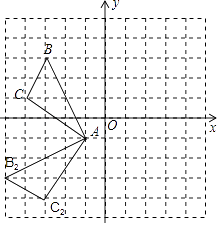
则点C的对应点C2的坐标是（﹣3，﹣4）
【解析】（1）补充成网格结构，然后找出点A、B、C关于y轴的对称点A1、B1、C1的位置，再顺次连接即可；再根据平面直角坐标系写出点B1的坐标；（2）根据旋转的性质画出△ABC绕点A按逆时针方向旋转90°后的△AB2C2 ， 写出点C2的坐标即可．
【考点精析】根据题目的已知条件，利用作轴对称图形的相关知识可以得到问题的答案，需要掌握画对称轴图形的方法：①标出关键点②数方格，标出对称点③依次连线．
科目：初中数学 来源： 题型：
【题目】下列语句中不正确的是（ ）
A.同一平面内，不相交的两条直线叫做平行线
B.在同一平面内，过一点有且只有一条直线与己知直线垂直
C.如果两个三角形，两条对应边及其夹角相等，那么这两个三角形全等
D.角是轴对称图形，它的角平分线是对称轴
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】阅读材料：求1+2+22+23+24+…+22013的值．
解：设S=1+2+22+23+24+…+22012+22013，将等式两边同时乘以2得：
2S=2+22+23+24+25+…+22013+22014
将下式减去上式得2S﹣S=22014﹣1
即S=22014﹣1
即1+2+22+23+24+…+22013=22014﹣1
请你仿照此法计算：
（1）1+2+22+23+24+…+210
（2）1+3+32+33+34+…+3n（其中n为正整数）．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】我们把分子为1的分数叫做单位分数，如
， 
， 
，…任何一个单位分数都可以拆分成两个不同的单位分数的和，如
， 
， 
，…
（1）根据对上述式子的观察，你会发现
，则a=________，b=________；
（2）进一步思考，单位分数
（n是不小于2的正整数），则x=________（用n的代数式表示）
（3）计算： 
．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】（请在括号里注明重要的推理依据）
如图，已知AM∥BN，∠A=60°．点P是射线AM上一动点（与点A不重合），BC、BD分别平分∠ABP和∠PBN，分别交射线AM于点C，D．
（1）求∠CBD的度数；
（2）当点P运动时，∠APB与∠ADB之间的数量关系是否随之发生变化？若不变化，请写出它们之间的关系，并说明理由；若变化，请写出变化规律．
（3）当点P运动到使∠ACB=∠ABD时，∠ABC的度数是 ．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某水果商行计划购进A、B两种水果共200箱，这两种水果的进价、售价如下表所示：
价格 | 进价（元/箱） | 售价（元/箱） |
A | 60 | 70 |
B | 40 | 55 |
（1）若该商行进贷款为1万元，则两种水果各购进多少箱？
（2）若商行规定A种水果进货箱数不低于B种水果进货箱数的 
，应怎样进货才能使这批水果售完后商行获利最多？此时利润为多少？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知AM∥CN，点B为平面内一点，AB⊥BC于B．
（1）如图1，直接写出∠A和∠C之间的数量关系________；
（2）如图2，过点B作BD⊥AM于点D，试说明：∠ABD=∠C；
（3）如图3，在（2）问的条件下，点E在DM上，且BE平分∠DBC，试说明∠ABE=∠AEB．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知二次函数y=﹣ 
x2﹣3x﹣ 
，设自变量的值分别为x1 ， x2 ， x3 ， 且﹣3＜x1＜x2＜x3 ， 则对应的函数值y1 ， y2 ， y3的大小关系是（ ）
A.y1＞y2＞y3
B.y1＜y2＜y3
C.y2＞y3＞y1
D.y2＜y3＜y1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com