Question

3．设△ABC的三边分别为a，b，c，p=$\frac{1}{2}$（a+b+c），则S_△ABC=$\sqrt{p（p-a）（p-b）（p-c）}$（海伦公式）或S_△ABC=$\sqrt{\frac{1}{4}[{a}^{2}{b}^{2}-（\frac{{a}^{2}+{b}^{2}-{c}^{2}}{2}）^{2}]}$（秦九韶公式）．
（1）请根据所学的知识对上述面积公式进行证明．
（2）若△ABC的三边长为5，6，7，△DEF的三边长为$\sqrt{5}$，$\sqrt{6}$，$\sqrt{7}$，请利用上面的两个公式分别求出△ABC和△DEF的面积．

Answer 1

分析 （1）作三角形高线AD，设未知数，由勾股定理列方程组表示出x、y的值，代入面积公式化简即可；
（2）因为三角形△ABC的三边长都是整数，所以代入海伦公式求面积，因为△DEF的三边长为无理数，它们的平方是整数，所以代入秦九韶公式求面积．

解答 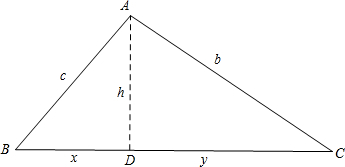解：（1）过A作AD⊥BC，垂足为D，设AD=h，BD=x，CD=y，
由题意可知：AB=c，BC=a，AC=b，
由勾股定理得：$\left\{\begin{array}{l}{x=a-y}\\{{h}^{2}={b}^{2}-{y}^{2}}\\{{h}^{2}={c}^{2}-{y}^{2}}\end{array}\right.$，
∴$\left\{\begin{array}{l}{x=\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2a}}\\{y=\frac{{a}^{2}-{c}^{2}+{b}^{2}}{2a}}\end{array}\right.$，
∴h=$\sqrt{{b}^{2}-{y}^{2}}$=$\sqrt{{b}^{2}-\frac{（{a}^{2}-{c}^{2}+{b}^{2}）^{2}}{4{a}^{2}}}$=$\frac{\sqrt{4{a}^{2}{b}^{2}-（{a}^{2}-{c}^{2}+{b}^{2}）^{2}}}{2a}$，
∴S_△ABC=$\frac{1}{2}$AD•BC，
=$\frac{1}{2}$a×h，
=$\frac{1}{2}$a×$\frac{\sqrt{4{a}^{2}{b}^{2}-（{a}^{2}-{c}^{2}+{b}^{2}）^{2}}}{2a}$，
=$\frac{1}{4}$$\sqrt{（2ab+{a}^{2}-{c}^{2}+{b}^{2}）（2ab-{a}^{2}+{c}^{2}-{b}^{2}）}$，
=$\sqrt{\frac{1}{16}[（a+b）^{2}-{c}^{2}]•[{c}^{2}-（a-b）^{2}]}$，
=$\sqrt{\frac{1}{2}（a+b+c）•\frac{1}{2}（a+b-c）•\frac{1}{2}（a+c-b）•\frac{1}{2}（b+c-a）}$，
=$\sqrt{p[\frac{1}{2}（a+b+c）-c]•[\frac{1}{2}（a+b+c）-b]•[\frac{1}{2}（a+b+c）-a]}$，
=$\sqrt{p（p-a）（p-b）（p-c）}$．
由上得：S_△ABC=$\frac{1}{2}$ah=$\sqrt{\frac{1}{4}{a}^{2}（{b}^{2}-{y}^{2}）}$=$\sqrt{\frac{1}{4}{a}^{2}[{b}^{2}-（\frac{{a}^{2}-{c}^{2}+{b}^{2}}{2a}）^{2}}$=$\sqrt{\frac{1}{4}[{a}^{2}{b}^{2}-（\frac{{a}^{2}+{b}^{2}-{c}^{2}}{2}）^{2}]}$（秦九韶公式）；
（2）若△ABC的三边长为5，6，7时，p=$\frac{1}{2}$（5+6+7）=9，
S_△ABC=$\sqrt{9×（9-5）（9-6）（9-7）}$=6$\sqrt{6}$，
△DEF的三边长为$\sqrt{5}$，$\sqrt{6}$，$\sqrt{7}$时，
S_△DEF=$\sqrt{\frac{1}{4}[（\sqrt{5}）^{2}（\sqrt{6}）^{2}-（\frac{5+6-7}{2}）^{2}]}$=$\frac{\sqrt{26}}{2}$．

点评 本题考查了二次根式的应用，熟练掌握二次根式的化简是关键，熟知以下几个公式：①$\sqrt{{a}^{2}}$=a（a≥0），②当a＞0，b≥0时，a$\sqrt{b}$=$\sqrt{{a}^{2}b}$，③当a＞0，b≥0时，$\sqrt{\frac{b}{a}}$=$\frac{\sqrt{ab}}{a}$，最后结果要化成最简二次根式的形式．