Question

14．如图，正方形ABCD的边长为1，点P在射线BC上（异于点B、C），直线AP与对角线BD及射线DC分别交于点F、Q
（1）若BP=$\frac{\sqrt{3}}{3}$，求∠BAP的度数；
（2）若点P在线段BC上，过点F作FG⊥CD，垂足为G，当△FGC≌△QCP时，求PC的长；
（3）以PQ为直径作⊙M．
①判断FC和⊙M的位置关系，并说明理由；
②当直线BD与⊙M相切时，直接写出PC的长．

Answer 1

分析 （1）在直角△ABP中，利用特殊角的三角函数值求∠BAP的度数；
（2）设PC=x，根据全等和正方形性质得：QC=1-x，BP=1-x，由AB∥DQ得$\frac{AB}{CQ}=\frac{BP}{PC}$，代入列方程求出x的值，因为点P在线段BC上，所以x＜1，写出符合条件的PC的长；
（3）①如图2，当点P在线段BC上时，FC与⊙M相切，只要证明FC⊥CM即可，先根据直角三角形斜边上的中线得CM=PM，则∠MCP=∠MPC，从而可以得出∠MCP+∠BAP=90°，再证明△ADF≌△CDF，
得∠FAD=∠FCD，则∠BAP=∠BCF，所以得出∠MCP+∠BCF=90°，FC⊥CM；
如图3，当点P在线段BC的延长线上时，FC与⊙M相切，同理可得∠MCD+∠FCD=90°，则FC⊥CM，FC与⊙M相切；
②当点P在线段AB上时，如图4，设⊙M切BD于E，连接EM、MC，设∠Q=x，根据平角BFD列方程求出x的值，作AP的中垂线HN，得∠BHP=30°，在Rt△BHP中求出BP的长，则得出PC=$\sqrt{3}$-1；当点P在点C的右侧时（即在线段BC的延长线上），如图5，同理可得：PC=$\sqrt{3}$+1．

解答 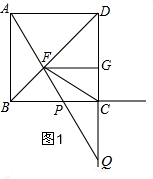解：（1）∵四边形ABCD是正方形，
∴∠ABP=90°，
∴tan∠BAP=$\frac{BP}{AB}$=$\frac{\frac{\sqrt{3}}{3}}{1}$=$\frac{\sqrt{3}}{3}$，
∵tan30°=$\frac{\sqrt{3}}{3}$，
∴∠BAP=30°；
（2）如图1，设PC=x，则BP=1-x，
∵△FGC≌△QCP，
∴GC=PC=x，DG=1-x，
∵∠BDC=45°，∠FGD=90°，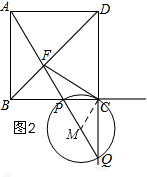
∴△FGD是等腰直角三角形，
∴FG=DG=CQ=1-x，
∵AB∥DQ，
∴$\frac{AB}{CQ}=\frac{BP}{PC}$，
∴$\frac{1}{1-x}=\frac{1-x}{x}$，
∴x=（1-x）²，
解得：x₁=$\frac{3+\sqrt{5}}{2}$＞1（舍去），x₂=$\frac{3-\sqrt{5}}{2}$，
∴PC=$\frac{3-\sqrt{5}}{2}$；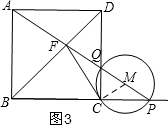
（3）①如图2，当点P在线段BC上时，FC与⊙M相切，理由是：
取PQ的中点M，以M为圆心，以PQ为直径画圆，连接CM，
∵∠PCQ=90°，PQ为直径，
∴点C是圆M上，
∵△PCQ为直角三角形，
∴MC=PM，
∴∠MCP=∠MPC，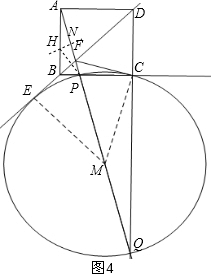
∵∠APB=∠MPC，
∴∠MCP=∠APB，
∵∠APB+∠BAP=90°，
∴∠MCP+∠BAP=90°，
∵AD=DC，∠ADB=∠CDB，FD=FD，
∴△ADF≌△CDF，
∴∠FAD=∠FCD，
∵∠BAP+∠FAD=∠BCF+∠FCD，
∴∠BAP=∠BCF，
∴∠MCP+∠BCF=90°，
∴FC⊥CM，
∴FC与⊙M相切；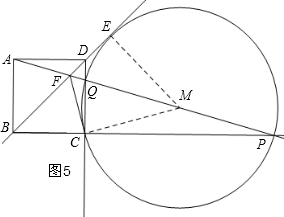
如图3，当点P在线段BC的延长线上时，FC与⊙M也相切，理由是：
取PQ的中点M，以M为圆心，以PQ为直径画圆，连接CM，
同理得∠AQD=∠MCQ，点C是圆M上，
∵AD=DC，∠BDA=∠CDB=45°，DF=DF，
∴△ADF≌△CDF，
∴∠FAD=∠FCD，
∵∠AQD+∠FAD=90°，
∴∠MCD+∠FCD=90°，
∴FC⊥MC，
∴FC与⊙M相切；
：②当点P在线段BC上时，如图4，
设⊙M切BD于E，连接EM、MC，
∴∠MEF=∠MCF=90°，
∵ME=MC，MF=MF，
∴△MEF≌△MCF，
∴∠QFC=∠QFE，
∵∠BAP=∠Q=∠BCF，
设∠Q=x，则∠BAP=∠BCF=x，∠QFE=∠QFC=45°+x，∠DFC=45°+x，
∵∠QFE+∠QFC+∠DFC=180°，
∴3（45+x）=180，
x=15，
∴∠Q=15°，
∴∠BAP=15°，
作AP的中垂线HN，交AB于H，交AP于N，
∴AH=AP，
∴∠BHP=30°，
设BP=x，则HP=2x，HB=$\sqrt{3}$x，
∴2x+$\sqrt{3}$x=1，
x=2-$\sqrt{3}$，
∴PC=BC-BP=1-（2-$\sqrt{3}$）=$\sqrt{3}$-1；
当点P在点C的右侧时（即在线段BC的延长线上），如图5，
同理可得：PC=$\sqrt{3}$+1；
综上所述：PC=$\sqrt{3}$-1或$\sqrt{3}$+1．

点评 本题是圆的综合题，综合考查了正方形、圆及切线、全等三角形的性质及判定；同时利用特殊的三角函数值求角的度数，本题还是动点问题，难度较大，尤其是第（3）问，因为不确定点P是在线段BC上还是在延长线上，有此情况存在，所以都要分情况进行讨论，从而分别证出结论或求出PC的长．