
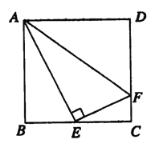
【题目】如图,在正方形![]() 中,
中,![]() 是
是![]() 的中点,
的中点,![]() 是
是![]() 上一点,
上一点,![]() ,则下列结论正确的有( )
,则下列结论正确的有( )
①![]() ②
②![]() ③
③![]() ④
④![]() ∽
∽![]()
A.1个B.2个C.3个D.4个
【答案】B
【解析】
由题中条件可得△CEF∽△BAE,进而得出对应线段成比例,进而又可得出△ABE∽△AEF,即可得出题中结论.
∵四边形ABCD是正方形,
∴∠B=∠C=90°,AB=BC=CD,
∵AE⊥EF,
∴∠AEF=∠B=90°,
∴∠BAE+∠AEB=90°,∠AEB+FEC=90°,
∴∠BAE=∠CEF,
∴△BAE∽△CEF,
∴![]()
∵![]() 是
是![]() 的中点,
的中点,
∴BE=CE
∴CE2=ABCF,∴②正确;
∵BE=CE=![]() BC,
BC,
∴CF=![]() BE=
BE=![]() CD,故③错误;
CD,故③错误;
∵![]()
∴∠BAE≠30°,故①错误;
设CF=a,则BE=CE=2a,AB=CD=AD=4a,DF=3a,
∴AE=2![]() a,EF=
a,EF=![]() a,AF=5a,
a,AF=5a,
∴![]()
∴![]()
∴△ABE∽△AEF,故④正确.
∴②与④正确.
∴正确结论的个数有2个.
故选:B.


 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系内,反比例函数和二次函数y=a(x2+x﹣1)的图象交于点A(1,a)和点B(﹣1,﹣a).
(1)求直线AB与y轴的交点坐标;
(2)要使上述反比例函数和二次函数在某一区域都是y随着x的增大而增大,求a应满足的条件以及x的取值范围;
(3)设二次函数的图象的顶点为Q,当Q在以AB为直径的圆上时,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市雷雷服饰有限公司生产了一款夏季服装,通过实验商店和网上商店两种途径进行销售,销售一段时间后,该公司对这种商品的销售情况,进行了为期30天的跟踪调查,其中实体商店的日销售量![]() (百件)与时间
(百件)与时间![]() (
(![]() 为整数,单位:天)的部分对应值如下表所示;网上商店的日销售量
为整数,单位:天)的部分对应值如下表所示;网上商店的日销售量![]() (百件)与时间
(百件)与时间![]() (
(![]() 为整数,单位:天)的关系如下图所示.
为整数,单位:天)的关系如下图所示.
时间 | 0 | 5 | 10 | 15 | 20 | 25 | 30 |
日销售量 | 0 | 25 | 40 | 45 | 40 | 25 | 0 |
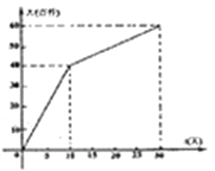
(1)请你在一次函数、二次函数和反比例函数中,选择合适的函数能反映![]() 与
与![]() 的变化规律,并求出
的变化规律,并求出![]() 与
与![]() 的函数关系式及自变量
的函数关系式及自变量![]() 的取值范围;
的取值范围;
(2)求![]() 与
与![]() 的函数关系式,并写出自变量
的函数关系式,并写出自变量![]() 的取值范围;
的取值范围;
(3)在跟踪调查的30天中,设实体商店和网上商店的日销售总量为![]() (百件),求
(百件),求![]() 与
与![]() 的函数关系式;当
的函数关系式;当![]() 为何值时,日销售总量
为何值时,日销售总量![]() 达到最大,并求出此时的最大值.
达到最大,并求出此时的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:求解一元一次方程,需要根据等式的基本性质,把方程转化为![]() 的形式;求解二元一次方程组,需要通过消元把它转化为一元一次方程来解;求解三元一次方程组,要把它转化为二元一次方程组来解;求解一元二次方程,需要把它转化为连个一元一次方程来解;求解分式方程,需要通过去分母把它转化为整式方程来解;各类方程的解法不尽相同,但是它们都用到一种共同的基本数学思想——转化,即把未知转化为已知来求解.
的形式;求解二元一次方程组,需要通过消元把它转化为一元一次方程来解;求解三元一次方程组,要把它转化为二元一次方程组来解;求解一元二次方程,需要把它转化为连个一元一次方程来解;求解分式方程,需要通过去分母把它转化为整式方程来解;各类方程的解法不尽相同,但是它们都用到一种共同的基本数学思想——转化,即把未知转化为已知来求解.
用“转化”的数学思想,我们还可以解一些新的方程.
例如,解一元三次方程![]() ,通过因式分解把它转化为
,通过因式分解把它转化为![]() ,通过解方程
,通过解方程![]() 和
和![]() ,可得原方程
,可得原方程![]() 的解.
的解.
再例如,解根号下含有来知数的方程:![]() ,通过两边同时平方把它转化为
,通过两边同时平方把它转化为![]() ,解得:
,解得:![]() . 因为
. 因为![]() ,且
,且![]() ,所以
,所以![]() 不是原方程的根,
不是原方程的根,![]() 是原方程的解.
是原方程的解.
(1)问题:方程![]() 的解是
的解是![]() ,
,![]() __________,
__________,![]() __________;
__________;
(2)拓展:求方程![]() 的解.
的解.
查看答案和解析>>
科目:初中数学 来源: 题型:
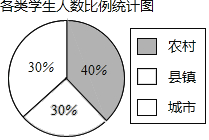
【题目】某市对九年级学生进行了一次学业水平测试,成绩评定分A、B、C、D四个等第.为了解这次数学测试成绩情况,相关部门从该市的农村、县镇、城市三类群体的学生中共抽取2000名学生的数学成绩进行统计分析,相应数据的统计图表如下:
各类学生成绩人数比例统计表
等第 人数 类别 | A | B | C | D |
农村 | 200 | 240 | 80 | |
县镇 | 290 | 132 | 130 | |
城市 | 240 | 132 | 48 |
(注:等第A、B、C、D分别代表优秀、良好、合格、不合格)
(1)请将上面表格中缺少的三个数据补充完整;
(2)若该市九年级共有15000名学生参加测试,试估计该市学生成绩合格以上(含合格)的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】京剧脸谱是京剧艺术独特的表现形式,现有三张不透明的卡片,其中两张卡片的正面图案为“红脸”,另外一张卡片的正面图案为“黑脸”,卡片除正面图案不同外,其余均相同,将这三张卡片背面向上洗匀,从中随机抽取一张,记录图案后放回,重新洗匀后再从中随机抽取一张.请用画树状图或列表的方法,求抽出的两张卡片上的图案都是“红脸”的概率(图案为“红脸”的两张卡片分别记为![]() 、
、![]() ,图案为“黑脸”的卡片记为
,图案为“黑脸”的卡片记为![]() ).
).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读以下材料,并按要求完成相应的任务.
已知平面上两点![]() ,则所有符合
,则所有符合![]() 且
且![]() 的点
的点![]() 会组成一个圆.这个结论最先由古希腊数学家阿波罗尼斯发现,称阿氏圆.
会组成一个圆.这个结论最先由古希腊数学家阿波罗尼斯发现,称阿氏圆.
阿氏圆基本解法:构造三角形相似.
(问题)如图1,在平面直角坐标中,在![]() 轴,
轴,![]() 轴上分别有点
轴上分别有点![]() ,点
,点![]() 是平面内一动点,且
是平面内一动点,且![]() ,设
,设![]() ,求
,求![]() 的最小值.
的最小值.

阿氏圆的关键解题步骤:
第一步:如图1,在![]() 上取点
上取点![]() ,使得
,使得![]() ;
;
第二步:证明![]() ;第三步:连接
;第三步:连接![]() ,此时
,此时![]() 即为所求的最小值.
即为所求的最小值.
下面是该题的解答过程(部分):
解:在![]() 上取点
上取点![]() ,使得
,使得![]() ,
,
又![]() .
.
任务:
![]() 将以上解答过程补充完整.
将以上解答过程补充完整.
![]() 如图2,在
如图2,在![]() 中,
中,![]() 为
为![]() 内一动点,满足
内一动点,满足![]() ,利用
,利用![]() 中的结论,请直接写出
中的结论,请直接写出![]() 的最小值.
的最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O是△ABC的外接圆,BC是⊙O的直径,D是劣弧![]() 的中点BD交AC于点E.
的中点BD交AC于点E.
(1)求证:AD2=DEDB.
(2)若BC=5,CD=![]() ,求DE的长.
,求DE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
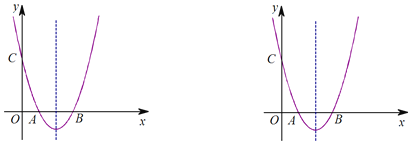
【题目】如图,在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,对称轴为直线
,对称轴为直线![]() ,点
,点![]() 的坐标为
的坐标为![]() .
.
(1)求该抛物线的表达式及顶点坐标;
(2)点![]() 为抛物线上一点(不与点
为抛物线上一点(不与点![]() 重合),联结
重合),联结![]() .当
.当![]() 时,求点
时,求点![]() 的坐标;
的坐标;
(3)在(2)的条件下,将抛物线沿平行于![]() 轴的方向向下平移,平移后的抛物线的顶点为点
轴的方向向下平移,平移后的抛物线的顶点为点![]() ,点
,点![]() 的对应点为点
的对应点为点![]() ,当
,当![]() 时,求抛物线平移的距离.
时,求抛物线平移的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com