
【题目】通过类比联想、引申拓展研究典型题目,可达到解一题知一类的目的.下面是一个案例.
原题:如图①,点 ![]() 分别在正方形
分别在正方形 ![]() 的边
的边 ![]() 上,
上, ![]() ,连接
,连接 ![]() ,则
,则 ![]() ,试说明理由.
,试说明理由.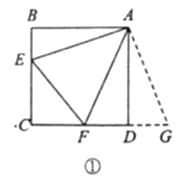
(1)思路梳理
因为 ![]() ,所以把
,所以把 ![]() 绕点
绕点 ![]() 逆时针旋转90°至
逆时针旋转90°至 ![]() ,可使
,可使 ![]() 与
与 ![]() 重合.因为
重合.因为 ![]() ,所以
,所以 ![]() ,点
,点 ![]() 共线.
共线.
根据 , 易证 ![]() , 得
, 得 ![]() .请证明.
.请证明.
(2)类比引申
如图②,四边形 ![]() 中,
中, ![]() ,
, ![]() ,点
,点 ![]() 分别在边
分别在边 ![]() 上,
上, ![]() .若
.若 ![]() 都不是直角,则当
都不是直角,则当 ![]() 与
与 ![]() 满足等量关系时,
满足等量关系时, ![]() 仍然成立,请证明.
仍然成立,请证明.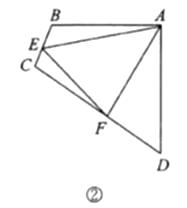
(3)联想拓展
如图③,在 ![]() 中,
中, ![]() ,点
,点 ![]() 均在边
均在边 ![]() 上,且
上,且 ![]() .猜想
.猜想 ![]() 应满足的等量关系,并写出证明过程.
应满足的等量关系,并写出证明过程.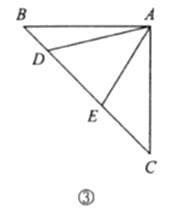
【答案】
(1)SAS;△AFE
(2)解:∠B+∠D=180°时,EF=BE+DF;
∵AB=AD,
∴把△ABE绕点A逆时针旋转90°至△ADG,可使AB与AD重合,
∴∠BAE=∠DAG,
∵∠BAD=90°,∠EAF=45°,
∴∠BAE+∠DAF=45°,
∴∠EAF=∠FAG,∵∠ADC+∠B=180°,
∴∠FDG=180°,点F、D、G共线,在△AFE和△AFG中,
∵AE=AG,∠FAE=∠FAG,AF=AF,
∴△AFE≌△AFG(SAS),
∴EF=FG,即:EF=BE+DF.
(3)解:猜想:DE2=BD2+EC2 , 理由如下:
根据ΔABD绕点A逆时针旋转90°得到ΔACD′,如图,连接ED′.
∴ΔABDΔACD′.
∴CD′=BD,AD′=AD,∠B=∠ACD′,∠BAD=∠D′ AC.
在RtΔABC中,
∵AB=AC,
∴∠ABC=∠ACB=45°.
∴∠ACB+∠ACD′=90°,即∠D′ CE=90°,
∴D’C2+CE2=D′E2 .
又∵∠DAE=45°,
∴∠BAD+∠EAC=45°.
∴∠D′AC+∠EAC=45°,即∠D′ AE=45°.∴ΔAD′ EΔADE,∴ED=ED′,
∴DE2=BD2+EC2 .
【解析】(1)解:∵AB=AD,∴把△ABE绕点A逆时针旋转90°至△ADG,可使AB与AD重合,∴∠BAE=∠DAG,∵∠BAD=90°,∠EAF=45°,∴∠BAE+∠DAF=45°,∴∠EAF=∠FAG,∵∠ADC=∠B=90°,∴∠FDG=180°,点F、D、G共线,在△AFE和△AFG中,∵AE=AG,∠EAF=∠FAG,AF=AF,∴△AFE≌△AFG(SAS),∴EF=FG,即:EF=BE+DF
(1)把△ABE绕点A逆时针旋转90°至△ADG,可使AB与AD重合,再证明△AFG≌△AFE进而得到EF=FG,即可得EF=BE+DF。
(2)∠B+∠D=180°时,EF=BE+DF,与(1)的证法类同。
(3)根据△AEC绕点A顺时针旋转90°得到△ABE′,根据旋转的性质,可知△AEC≌△ABE′得到BE′=EC,AE′=AE,∠C=∠ABE′,∠EAC=∠E′AB,根据Rt△ABC中的,AB=AC得到∠E′BD=90°,所以E′B2+BD2=E′D2 , 证△AE′D≌△AED,利用DE=DE′得到DE2=BD2+EC2。


 全能测控一本好卷系列答案
全能测控一本好卷系列答案科目:初中数学 来源: 题型:
【题目】如图, ![]() ,已知
,已知 ![]() 中,
中, ![]() ,
, ![]() 的顶点A,B分别在边OM,ON上,当点B在边ON上运动时,点A随之在边OM上运动,
的顶点A,B分别在边OM,ON上,当点B在边ON上运动时,点A随之在边OM上运动, ![]() 的形状保持不变,在运动过程中,点C到点O的最大距离为.
的形状保持不变,在运动过程中,点C到点O的最大距离为.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中,正确的是( )
A.因为相反数是成对出现的,所以0没有相反数B.数轴上原点两旁的两点表示的数是互为相反数
C.符号不同的两个数是互为相反数D.正数的相反数是负数,负数的相反数是正数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一楼房AB后有一假山,其坡度为i=1: ![]() ,山坡坡面上E点处有一休息亭,测得假山坡脚C与楼房水平距离BC=25米,与亭子距离CE=20米,小丽从楼房顶测得E点的俯角为45°,求楼房AB的高.(注:坡度i是指坡面的铅直高度与水平宽度的比)
,山坡坡面上E点处有一休息亭,测得假山坡脚C与楼房水平距离BC=25米,与亭子距离CE=20米,小丽从楼房顶测得E点的俯角为45°,求楼房AB的高.(注:坡度i是指坡面的铅直高度与水平宽度的比)
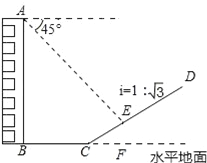
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法不正确的是( )
A. 数据3、5、4、1、﹣2的中位数是3
B. 数据1、1、0、2、4的平均数是2
C. 在选举中,人们通常最关心是数据的众数
D. 甲乙两人近5次数学考试平均分都是95分,方差分别是2.5和8.5,要选一人参加数学竞赛,选甲比较合适
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com