
将两块三角板如图放置,其中∠C=∠EDB=![]() ,∠A=
,∠A=![]() ,∠E=
,∠E=![]() ,AB=DE=6.求重叠部分四边形DBCF的面积.
,AB=DE=6.求重叠部分四边形DBCF的面积.

|
答案:在△EDB中, 因为∠EDA= 所以DB=DE· 所以AD=AB-DB=6-2 又因为∠A= 所以∠AFD= 所以S△ADF= 在等腰直角三角形ABC中,斜边AB=6, 所以S△ABC= 所以S四边形DBCF=S△ABC-S△ADF=9-(24-12 剖析:要求四边形DBCF的面积,而这个四边形不是特殊的四边形,故关键在于把它转化为几个特殊多边形的和或差再计算. |
|
本题还可以连接BF,把四边形分成两个三角形之和,你能用这种方法计算出来吗? |


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案科目:初中数学 来源: 题型:
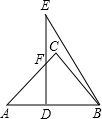 (2013•宝山区一模)将两块三角板如图放置,其中∠C=∠EDB=90°,∠A=45°,∠E=30°,AB=DE=12,求重叠部分四边形DBCF的面积.
(2013•宝山区一模)将两块三角板如图放置,其中∠C=∠EDB=90°,∠A=45°,∠E=30°,AB=DE=12,求重叠部分四边形DBCF的面积.查看答案和解析>>
科目:初中数学 来源:《第1章 解直角三角形》2009年单元过关测试(A卷)(解析版) 题型:解答题
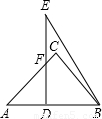
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com