
°æƒø°ø»ÁÕº1À˘ 棨A°¢B¡Ωµ„Õ¨ ±¥”‘≠µ„O≥ˆ∑¢£¨µ„A“‘√ø√Îx∏ˆµ•Œª≥§∂»—ÿx÷·µƒ∏∫∑ΩœÚ‘À∂Ø£¨µ„B“‘√ø√Îy∏ˆµ•Œª≥§∂»—ÿy÷·µƒ’˝∑ΩœÚ‘À∂Ø£Æ

£®1£©»Ù|x+2y-10|+|2x-y|=0£¨ ‘∑÷±«Û≥ˆ1√Î÷”∫Û°˜AOBµƒ√ʪ˝£ª
£®2£©»ÁÕº2£¨À˘ 棨…Ë°œBAOµƒ¡⁄≤πΩ«∫Õ°œABOµƒ¡⁄≤πΩ«µƒ∆Ω∑÷œþœýΩª”⁄µ„P£¨Œ £∫µ„A°¢B‘⁄‘À∂صƒπ˝≥Ã÷–£¨°œPµƒ¥Û–° «∑Òª·∑¢…˙±‰ªØ£ø»Ù≤ª∑¢…˙±‰ªØ£¨«Î«Û≥ˆ∆‰÷µ£ª»Ù∑¢…˙±‰ªØ£¨«ÎÀµ√˜¿Ì”…£ª
£®3£©»ÁÕº3À˘ 棨—”≥§BA÷¡E£¨‘⁄°œABOµƒƒ⁄≤ø◊˜…‰œþBFΩªx÷·”⁄µ„C£¨»Ù°œEAC°¢°œFCA°¢°œABCµƒ∆Ω∑÷œþœýΩª”⁄µ„G£¨π˝µ„G◊˜BEµƒ¥πœþ£¨¥π◊„Œ™H£¨…Ë°œAGH=¶¡£¨°œBGC=¶¬£¨ ‘ÃΩæø≥ˆ¶¡∫Õ¶¬¬˙◊„µƒ ˝¡øπÿœµ≤¢∏¯≥ˆ÷§√˜£Æ
°æ¥∞∏°ø£®1£©1√Î÷”∫Û°˜AOBµƒ√ʪ˝=4£ª£®2£©µ„A°¢B‘⁄‘À∂صƒπ˝≥Ã÷–£¨°œPµƒ¥Û–°≤ª±‰£¨°œP=45°„£¨¿Ì”…º˚Ω‚Œˆ£ª£®3£©¶¡=¶¬£¨¿Ì”…º˚Ω‚Œˆ.
°æΩ‚Œˆ°ø
£®1£©Ω‚∂˛‘™“ª¥Œ∑Ω≥Ã◊È«Û≥ˆx°¢y£¨µ√µΩOA°¢OBµƒ≥§£¨∏˘æð»˝Ω«–Œµƒ√ʪ˝π´ Ωº∆À„£¨µ√µΩ¥∞∏£ª
£®2£©∏˘æðΩ«∆Ω∑÷œþµƒ∂®“µ√µΩ°œPAB=![]() °œEAB£¨°œPBA=
°œEAB£¨°œPBA=![]() °œFBA£¨∏˘æð»˝Ω«–Œƒ⁄Ω«∫Õ∂®¿Ìº∆À„º¥ø…£ª
°œFBA£¨∏˘æð»˝Ω«–Œƒ⁄Ω«∫Õ∂®¿Ìº∆À„º¥ø…£ª
£®3£©◊˜GM°ÕBF”⁄µ„M£¨∏˘æð»˝Ω«–ŒµƒÕ‚Ω«–‘÷ °¢÷±Ω«»˝Ω«–Œµƒ–‘÷ º∆À„£Æ
£®1£©”…“‚µ√£¨![]() £¨
£¨
Ω‚µ√£¨![]() £¨
£¨
”…“‚µ√£¨1√Î÷”∫ÛOA=2£¨OB=4£¨
‘Ú1√Î÷”∫Û°˜AOBµƒ√ʪ˝= ![]() °¡2°¡4=4£ª
°¡2°¡4=4£ª
£®2£©µ„A°¢B‘⁄‘À∂صƒπ˝≥Ã÷–£¨°œPµƒ¥Û–°≤ª±‰£¨°œP=45°„£¨
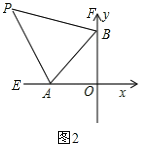
¿Ì”…»Áœ¬£∫°þ°œAOB=90°„
°ý°œOAB+°œOBA=90°„
°ý°œEAB+°œFBA=270°„£¨
°þAP∆Ω∑÷°œEAB£¨
°ý°œPAB=![]() °œEAB£¨
°œEAB£¨
Õ¨¿Ì£¨°œPBA=![]() °œFBA£¨
°œFBA£¨
°ý°œPAB+°œPBA=![]() £®°œEAB+°œFBA£©=135°„£¨
£®°œEAB+°œFBA£©=135°„£¨
°ý°œP=180°„-135°„=45°„£ª
£®3£©¶¡=¶¬£¨
¿Ì”…»Áœ¬£∫◊˜GM°ÕBF”⁄µ„M£¨
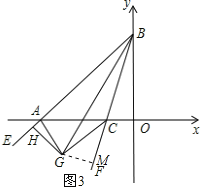
°œAGH=90°„- ![]() °œEAC
°œEAC
=90°„- ![]() £®180°„-°œBAC£©
£®180°„-°œBAC£©
= ![]() °œBAC£¨
°œBAC£¨
°œBGC=°œBGM-°œCGM
=90°„-![]() °œABC-£®90°„-
°œABC-£®90°„-![]() °œACF£©
°œACF£©
= ![]() £®°œACF-°œABC£©
£®°œACF-°œABC£©
= ![]() °œBAC
°œBAC
°ý°œAGH=°œBGC£¨º¥¶¡=¶¬£Æ



| ƒÍº∂ | ∏þ÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏þ“ª | ∏þ“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ∂˛ | ∏þ∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ»˝ | ∏þ»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨BD «°˜ABCµƒΩ«∆Ω∑÷œþ,AEÅABDΩªBDµƒ'—”≥§œþ”⁄µ„E, °œABC = 72°„£¨°œC£∫°œADB =2£∫3,«Û°œBAC ∫Õ°œDAE µƒ∂» ˝.
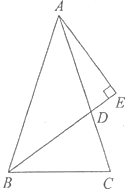
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕºÀ˘ 棨AB°¢CDœýΩª”⁄µ„O£¨»ÙBE∆Ω∑÷°œABDΩªCD”⁄F£¨CE∆Ω∑÷°œACDΩªAB”⁄G£¨°œA=45°„£¨°œBEC=40°„£¨‘Ú°œDµƒ∂» ˝Œ™____£Æ

≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨°œBAC=°œDAF=90°„£¨AB£ΩAC£¨AD£ΩAF£¨µ„D£¨EŒ™BC±þ…œµƒ¡Ωµ„£¨«“°œDAE£Ω45°„£¨¡¨Ω”EF£¨BF£¨‘Úœ¬¡–Ω·¬€£∫¢Ÿ°˜AFB°’°˜ADC£ª¢⁄°˜ABDŒ™µ»—¸»˝Ω«–Œ£ª¢€°œADC=120°„£ª¢ÐBE2£´DC2=DE2£¨∆‰÷–’˝»∑µƒ”–( )∏ˆ

A.4B.3C.2D.1
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕºÀ˘ 棨±þ≥§Œ™2µƒµ»±þ»˝Ω«–ŒABC÷–£¨Dµ„‘⁄±þBC…œ‘À∂Ø(≤ª”ÎB°¢C÷ÿ∫œ)£¨µ„E‘⁄±þABµƒ—”≥§œþ…œ£¨µ„F‘⁄±þACµƒ—”≥§œþ…œ£¨AD=DE=DF.
(1)»Ù°œAED=30°„£¨‘Ú°œADB=_______°„.
(2)«Û÷§£∫°˜BED°’°˜CDF
(3)µ„D‘⁄BC±þ…œ¥”B÷¡Cµƒ‘À∂Øπ˝≥Ã÷–£¨°˜BED÷Ð≥§±‰ªØπʬ…Œ™( )
A.≤ª±‰ B.“ª÷±±‰–° C.œ»±‰¥Û∫Û±‰–° D.œ»±‰–°∫Û±‰¥Û

≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨‘⁄°˜ABC÷–£¨°œBAC£Ω90°„£¨∑÷±“‘AC£¨BCŒ™±þ≥§£¨‘⁄»˝Ω«–ŒÕ‚◊˜’˝∑Ω–ŒACFG∫Õ’˝∑Ω–ŒBCED£Æ»ÙAC£Ω4£¨AB£Ω6£¨‘ÚEF£Ω______£Æ
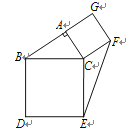
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øµØª…π“…œŒÔÃÂ∫Ûª·…Ï≥§£¨»Ù“ªµØª…≥§∂»(cm)”ÎÀ˘π“ŒÔÃÂ÷ ¡ø(kg)÷ƺ‰µƒπÿœµ»Áœ¬±Ì£∫
ŒÔõƒ÷ ¡ø(kg) | 0 | 1 | 2 | 3 | 4 | 5 |
µØª…µƒ≥§∂»(cm) | 12 | 12£Æ5 | 13 | 13£Æ5 | 14 | 14£Æ5 |
‘Úœ¬¡–Àµ∑®¥ÌŒÛµƒ «£® £©
A.µØª…≥§∂»ÀÊŒÔõƒ÷ ¡øµƒ±‰ªØ∂¯±‰ªØ£¨ŒÔõƒ÷ ¡ø «◊‘±‰¡ø£¨µØª…µƒ≥§∂» «“Ú±‰¡ø
B.»Áπ˚ŒÔõƒ÷ ¡øŒ™x kg£¨ƒ«√¥µØª…µƒ≥§∂»y cmø…“‘±Ì 挙y=12+0.5x
C.‘⁄µØª…ƒÐ≥– еƒ∑∂Œßƒ⁄£¨µ±ŒÔõƒ÷ ¡øŒ™7kg ±£¨µØª…µƒ≥§∂»Œ™16cm
D.‘⁄√ªπ“ŒÔà±£¨µØª…µƒ≥§∂»Œ™12cm
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨‘⁄’˝∑Ω–ŒABCD÷–£¨AB=2£¨—”≥§BCµΩµ„E£¨ πCE=1£¨¡¨Ω”DE£¨∂ص„P¥”µ„A≥ˆ∑¢“‘√ø√Î1∏ˆµ•ŒªµƒÀŸ∂»—ÿAB-BC-CD-DAœÚ÷’µ„A‘À∂Ø£¨…˵„Pµƒ‘À∂Ø ±º‰Œ™t√Σ¨µ±°˜ABP∫Õ°˜DCE»´µ» ±,tµƒ÷µ____.

≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨¥Û ˜AB”Î¥Û ˝CDœýæý13m£¨–°ª™¥”µ„B—ÿBC◊þœÚµ„C£¨––◊þ“ª∂Œ ±º‰∫ÛÀ˚µΩ¥Ôµ„E£¨¥À ±À˚—ˆÕ˚¡Ωø√¥Û ˜µƒ∂•µ„A∫ÕD£¨¡ΩÃı ”œþµƒº–Ω«’˝∫√Œ™90°„£¨«“EA=ED.“—÷™¥Û ˜ABµƒ∏þŒ™5m£¨–°ª™––◊þµƒÀŸ∂»Œ™1m/s£¨–°ª™––◊þµΩµ„Eµƒ ±º‰ «£® £©

A. 13s B. 8s C. 6s D. 5s
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
∞Ÿ∂»÷¬–≈ - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒÞ÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com