
如图,在正方形ABCD中,P是对角线AC上的一点,连接BP、DP,延长BC到E,使PB=PE.求证:∠PDC=∠PEC.

科目:初中数学 来源: 题型:
某公司承担了制作600个上海世博会道路交通指引标志的任务,原计划x天完成,实际平均每天多制作了10个,因此提前5天完成任务.根据题意,下列方程正确的是( )
A. 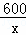 ﹣
﹣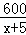 =10 B.
=10 B.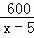 ﹣
﹣ =10 C
=10 C  ﹣
﹣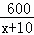 =5 D.
=5 D. 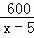 +10=
+10=
查看答案和解析>>
科目:初中数学 来源: 题型:
已知△ABC的三边长分别为 ,
, ,2,△A′B′C′的两边长分别是1和
,2,△A′B′C′的两边长分别是1和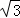 ,如果△ABC与△A′B′C′相似,那么△A′B′C′的第三边长应该是( )
,如果△ABC与△A′B′C′相似,那么△A′B′C′的第三边长应该是( )
A.  B.
B.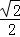 C.
C.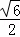 D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,⊙O是△ABC的外接圆,AB为直径,OD∥BC交⊙O于点D,交AC于点E,连接AD,BD,CD .
.
(1)求证:AD=CD;
(2)若AB=10,cos∠ABC=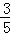 ,求tan∠DBC的值.
,求tan∠DBC的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com